Signal Outages in Fading Channels
The mobile Rayleigh or Rician radio channel
is characterized by rapidly changing channel characteristics. As typically a certain minimum (threshold) signal level is needed for acceptable communication performance, the received signal will experience periods of
- sufficient signal strength or "non-fade intervals"
- insufficient signal strength or "fades"
During fades the user experiences a signal outage.
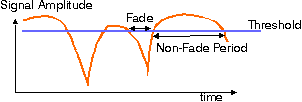
Figure: Signal outages occur during channel fades. See also: Gilbert-Elliot model
|
| 
| The signal outage probability is fairly simple to compute if one knows the probability
distribution of the fading (e.g. Rayleigh or Rician / Nakagami) and outage occurs if
the signal drops below the noise power level.
The derivation involves an integration over the pdf of wanted and interfering signal power. |
|
|
|
|
The link budget calculation provides
an estimate of the margin for how deep a signal fade can be, before the receiver looses the signal.
|
|
|
| The calculation becomes much more complicated if the (multiple) interfering signals also exhibit fading. Moreover shadowing affects the outage probability also.
|
Outage Probability versus Efficiency
A crucial aspect in the evaluation and planning of radio networks is the computation of the effect
of co-channel interference in radio links. The amount of interference that can be tolerated
determines the required separation distance between co-channel cells and therefore also the
efficiency of the network. The link performance of cellular telephone networks was first studied
around 1980 by Gosling, French and Cox. Initial analyses were limited to outage
probabilities in continuous wave (CW) voice communication, taking into account path loss and
flat (frequency non-selective) Rayleigh fading. In the 1980's the technique for computing outage
probabilities was refined step by step, considering among other things
shadowing, multiple interfering signals
cumulating coherently or, more realistically,
incoherently, the modulation technique and error correction method, and more recently
the presence of a dominant line-of-sight
propagation path, as it occurs in micro-cellular networks.
The stochastic occupation of nearby co-channel cells according to the traffic laws by
Erlang was included in some studies.
Computational Results
Any cellular operator will use topographic data bases to estimate outage probabilities
in the area covered by the telephone service, but results for idealized hexagonal cell layouts are
nonetheless illustrative for the effect of the reuse distance and shadowing.
Evidently, the operator can reduce the outage probability by choosing larger reuse distances. However,
this requires large cluster sizes, which results in poor spectrum efficiency.
| |
 |
|
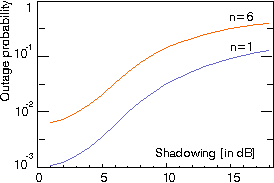
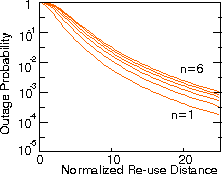
Figure: Outage probability versus degree of shadow fading
for 1 and 6 interfering signals. Shadowing 6 dB. Receiver threshold 10 dB.
Reuse distance equal 10 times the cell radius. Plane earth loss (40 log d).
|
|
For a crude propagation model that does not include
terrain data, the standard deviation of the error is about 12 dB.
In such case, either unacceptably large outage probabilities would be experienced
or the cluster size would have to be unacceptable large. Hence, improved cell planning
is required and virtually no operator plans its services considering idealized hexagonal cells.
Mostly topographical data bases are used to estimate the area-mean signal power and interference powers
as accurately as possible.
Computational Methods
Computation of the outage probability requires that we find the probability that
the signal-to-interference ratio drops below a certain threshold.
See: derivation.
As all (fading) signals
have fluctuating signal powers, this mean that we must integrate over the probability density functions
of all signals involved.
- fading and shadowing of the wanted signal
- fading and shadowing of each interfering signal. Mostly it is assumed that
- interfering signals fade independently and independent of the wanted signal
- interfering signal powers accumulate incoherently, i.e., that is we may add powers.
In such case the pdf of the total interference power is the convolution of the pdf power
of individual interfering signals
The number of interfering signals is six in a typical hexagonal reuse pattern, but interfering signals
may use discontinuous voice transmission. In such case the terminal switches of the carrier during speech pauses to reduce the amount of interference caused to other users.
Mathematical Background
In the special case that the wanted signal is Rayleigh fading, the received wanted signal is exponentially distributed.
That implies that our integration can be rewritten as a Laplace transformation. The outage probability becomes
P(outage) = 1 - P(C/I > z) = 1 - Laplace(f ; z /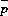 
)
where
- C/I is the signal-to-interference ratio
- z is the minimum required C/I ratio
- f is the pdf of total interference power
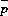- is the local-mean power of the wanted signal
- Laplace(g ; s) is the Laplace image of function g,
evaluated in the point s.
Click here for a discussion of how to
write a PASCAL program
that computes the outage probability in a channel with Rayleigh fading and shadowing.
Generic Expressions
Similar expressions can be found for Rician and Nakagami fading wanted signals.
A generic expression exists that is suitable for rapid computer evaluation.
(Note: Use of the Nakagami or gamma distribution
to approximate a Rician distribution appeared inaccurate and overly optimistic.)
