JPL's Wireless Communication Reference Website Chapter: Wireless Channels Section: Multipath fading

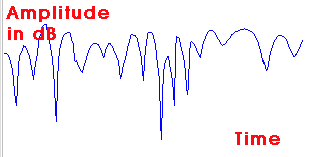
A sample of a Rayleigh fading signal. Signal amplitude (in dB) versus time for an antenna moving at constant velocity. Notice the deep fades that occur occasionally. Although fading is a random process, deep fades have a tendency to occur approximately every half a wavelength of motion. See also: More samples of channels Simulation and animation of Rayleigh fading

Next we'll discuss the basic mechanisms of mobile reception.

Effect of Motion

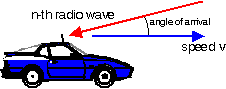
The Doppler shift of this wave is

,

where v is the speed of the antenna.

Phasor representation

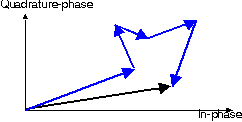
Figure: Phasor diagram of a set of scattered waves (in blue), resulting a Rayleigh-fading envelope (in black). Animation.

In case of an unmodulated carrier, the transmitted signal has the form

.

The received unmodulated signal r(t) can be expressed as

An inphase-quadrature representation of the form

can be found with in-phase component

and quadrature phase component

.

(Quasi-) Stationary Channel Snapshot

and

Thus both the inphase and quadrature component, I(t) and Q(t) can be interpreted as the sum of many (independent) small contributions. Each contribution is due to a particular reflection, with its own amplitude c_n and phase. For sufficiently many reflections (large N), the Central Limit Theorem now says that the inphase and quadrature components tend to a Gaussian distribution of their amplitude. I(t) and Q(t) appear to be independent and identically distributed (iid).

Note also that if the antenna speed is set to zero, channel fluctuations no longer occur. Fading is due to motion of the antenna. An exception occurs if reflecting objects move. In a vehicular cellular phone system, the user is likely to move out of a fade, but in a Wireless LAN, a terminal may by accident be placed permanently in a fade where no reliable coverage is available.

Elaboration of this model

	Parameter	Probability Distribution
	I(t1) and Q(t1) components	i.i.d. Gaussian, Zero mean
	I(t1) and Q(t2) components at time offset	Correlated jointly Gaussian
	I(t2) given I(t1)	Gaussian
	Amplitude r	Rayleigh
	r(t2) given r(t1)	Rician
	Derivative of Amplitude	Gaussian Independent of amplitude
	Phase	Uniform
	Derivative of Phase	Gaussian Dependent on amplitude
	Power	exponential

This propagation model allows us, for instance,

• to compute the probability density function of the received amplitude.
• to compute the Doppler spread and the rate of channel fluctuations.
• to build a channel simulator (see also a Javaź animation)
• to predict the effect of multiple interfering signals in a mobile channel
• to find outage probabilities in a cellular network

If the set of reflected waves are dominated by one strong component, Rician fading is a more appropriate model.

JPL's Wireless Communication Reference Website © 1993, 1995, 1999.