
 |
JPL's Wireless Communication Reference WebsiteChapter: Telephony Systems
|
Laplace images of probability density functions are particularly useful in the evaluation of the joint power received from multiple interfering signals:
The pdf of the sum of powers of multiple signals is the convolution of the pdf of each component. After
Laplace transformation, this convolution goes into a multiplication
The one-sided Laplace transform of a function f(x) is defined as the integral from zero to infinity over f(x) exp(-sx) , where s is the image variable.
Moreover, Laplace images are closely related to 'moment-generating functions' and 'characteristic functions' used in probability theory, although mostly the kernel 'exp(-jsx)' with j = SQRT(-1) is used for characteristic functions, rather than 'exp(-sx)'.
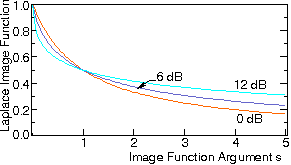
Figure: Laplace image of the pdf of received power from Rayleigh fading
and shadowed interferer.
Various degrees of shadowing.
It can easily be shown that the probability that the power of a Rayleigh fading wanted signal sufficiently exceeds the power of an interferer equals the Laplace transform of the pdf of interference power, observed in one point. That is, the outage probability is found as a particular point on the above curve.
For Nakagami and Rician fading wanted signals the expression for outage probability is more complicated: it a series of Laplace transforms and derivatives of Laplace transforms