|
|
JPL's Wireless Communication Reference WebsiteChapter: Wireless Propagation
Channels
|
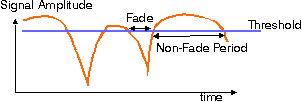A simple model to estimate the probability of succussfully receiving a data packet over a fading channel assumes that
the fading is memoryless. i.e., transitions from fade to non-fade periods occur randomly without any influence of how long the channel is already in a fade or non-fade interval. Relatively simple expressions exist for the average fade duration, while it is much more difficult to derive the precise distribution of fade durations. However the approximation as exponentially distrubuted durations appears reasonable.
The channel state can than be modelled as a Markov chain with a fade (good) and non-fade (poor) state. Packet transmissions are assumed to be successfull whenever the transmission starts in a non-fade interval and that non-fade interval lasts for the full duration of the transmission.
 |
SNR below the ThresholdIn the "poor" or "fade" state, the signal-to-noise or signal-to-interference ratio is insufficient to support reliable communication. The bit error rate is about one half. The probability of being in this state is the outage probability Pout. The transition rate of moving out of this state is 1/(AFD) with AFD the average fade duration. Pout = AFD * TCR, with TCR the threshold crossing rate. | ||
 |
SNR above the ThresholdIn the "good" or "non-fade" state, communication is reliable with negligible error rates. In practice, the duration of a non-fade period often corresponds to a motion of about half a wavelength. That is, the spread is much less than one would expect from an exponential distribution (from memoryless transitions). This is due to peaks in the Doppler spectrum, near + and - the maximum Doppler shift. |
This model provided the basics for calculating various radio link performance aspects.
 |
Temporal aspects of fading Effective throughput |
