JPL's Wireless Communication Reference Website

Chapter: Cellular Telephone Networks.

Principles of cellular frequency reuse

In the cellular concept, frequencies allocated to the service are re-used in a regular pattern of areas, called 'cells', each covered by one base station. In mobile-telephone nets these cells are usually hexagonal. In radio broadcasting, a similar concept has been developed based on rhombic cells.

To ensure that the mutual interference between users remains below a harmful level, adjacent cells use different frequencies. In fact, a set of C different frequencies {f1, ..., fC} are used for each cluster of C adjacent cells. Cluster patterns and the corresponding frequencies are re-used in a regular pattern over the entire service area.


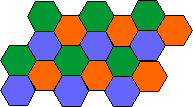Frequency reuse plan for C = 3, with hexagonal cells. (i=1, j =1)


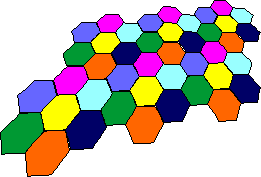Frequency reuse plan for C = 7 (i=2, j =1).

The total bandwidth for the system is C times the bandwidth occupied by a single cell.

Real-World Cells

In the practice of cell planning, cells are not hexagonal as in the theoretical studies. Computer methods are being used for optimised planning of base station location and cell frequencies. Pathloss and link budgets are computed from the terrain features and antenna data. This determines to coverage of each base station and interference to other cells.

Source: Siemens TORNADO D Cellular Planning Tool

Reuse Distance

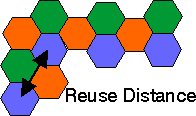 The closest distance between the centres of two cells using the same frequency (in different clusters) is determined by the choice of the cluster size C and the lay-out of the cell cluster. This distance is called the frequency 're-use' distance. It can be shown that the reuse distance ru, normalised to the size of each hexagon, is 
  ru = SQRT{3 C}

For hexagonal cells, i.e., with 'honeycomb' cell lay-outs commonly used in mobile radio, possible cluster sizes are C = i2 + ij + j2, with integer i and j (C = 1, 3, 4, 7, 9, ...). Integers i and j determine the relative location of co-channel cells.


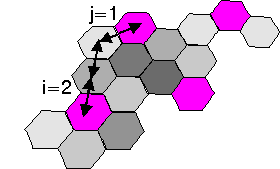
7-cell reuse with i = 2 and j =1.

Derivation

Listen to an animated audio presentation by Jean-Paul Linnartz (embedded html, SMIL, PPT-only)

Also, for more details on the math behind hexagonal cell layouts, check this pdf document.

Exercise

Show that ru = SQRT {3(i2 + ij + j2)}.
Compute the surface area of a cluster of cells, both in terms of Use these two expressions to verify that C = i2 + ij + j2. Answer.

In practical FM or digital cellular networks for public radio telephony, the cluster size mostly is on the order of C = 7 or 9, though with special techniques, such as diversity reception, smaller re-use distances can be used. GSM can work with C = 3 or 4.

Cellular CDMA systems can use C = 1, i.e., the same frequency is used in all cells.

Spectrum Efficiency

In most cellular systems, each base station can carry more than one telephone call in its cell. If the number of parallel channels per base station is denoted by M, the total bandwidth for the cellular net Bs is the product of the occupied bandwidth per channel BT, the number of channels per cell M and the cluster size C. Thus Bs = M C BT. The spectrum efficiency SE of a cellular net can be defined as the carried traffic per cell Ac, expressed in erlang, divided by the bandwidth of the total system Bs and divided by the area of a cell Su. So 


           Ac     
SE =  ----------- 
      BT C M Su
Here, Ac is mostly computed from Erlang B formulas, with Ac equals the attempted traffic multiplied by the probability of success (= 1 - blocking probability).

Mostly, the spectrum efficiency is expressed in erlang/MHz/km2.

Thus, we observe that the spectrum efficiency decreases with the cluster size C. System performance, for instance expressed in terms of the outage probability or the bit error rate experienced by the user, improves with increasing re-use distance, so it improves with the cluster size. Hence, achieving high system performance and efficient use of the radio spectrum are conflicting objectives for a network designer.

Erlang B Calculator

Input parameters:
Number of available
radio carriers per cell: 		carrier / cell
Number of channels
per radio carrier: 		users / carrier
Blocking percentage: %
Cluster size: cells/cluster
Channel spacing /
Transmit bandwidth: 		kHz
Cell radius km

Run calculation:

  

Results:
Traffic per cell:erlang/cell
Spectrum efficiency erlang/MHz/cell
 

erlang/MHz/km2
Default values have been inspired by GSM.

Disclaimer: Executable software programmes are provided with no guarantee whatsoever. See License.

Exercise

Explain why operators of cellular networks in densely populated areas prefer to put their base stations in the valleys, rather than on top of mountains. How does this differ from the situation in rural areas? (see answer)

Broadcast Networks

The concept of regular frequency reuse patterns is also used for broadcast transmitters. One example is the planning of local (30 watt) radio stations in The Netherlands and Belgium. The channel spacing 100 kHz. Frequencies used are 105 MHz + k * 100 kHz, where k is the channel number in the following figure.


Figure: Typical 31- frequency reuse pattern for FM radio (CCIR).

contents chapter next

JPL's Wireless Communication Reference Website © 1993, 1995, 1997.