Comparing Rician and Nakagami Fading

Rice and Nakagami fading are two generalisations of the model for Rayleigh fading. In literature, often a Nakagami model is used for analytical simplicity in cases where Rician fading would be a more appropriate model. In contrast to common belief, the Nakagami model is not an appropriate approximation for Rician fading. It has an essentially different behaviour for deep fades, such that results on outage probabilities or error rates can differ by orders of magnitude.

Rician Models

To describe microcellular propagation, the Rayleigh model lacked the effect of a dominant line-of-sight component, and Rician model appeared to be more appropriate. For analytical and numerical evaluation of system performance, the expressions for Rician fading are less convenient, mainly due to the occurrence of a Bessel function in the Rician probability density function of received signal amplitude. Approximations by a Nakagami distribution, with simpler mathematical expressions have become popular.

Nakagami Models

The Nakagami fading model was initially proposed because it matched empirical results for short wave ionospheric propagation. In current wireless communication, the main role of the Nakagami model can be summarized as follows

It describes the amplitude of received signal after maximum ratio diversity combining.
The sum of multiple independent and identically distributed (i.i.d.) Rayleigh-fading signals have a Nakagami distributed signal amplitude. This is particularly relevant to model interference from multiple sources.
The Nakagami distribution matches some empirical data better than other models
The Rician and the Nakagami model behave approximately equivalently near their mean value. This observation has been used in many recent papers to advocate the Nakagami model as an approximation for situations where a Rician model would be more appropriate.

Comparison

In the analysis of outage probabilities or error rates, it is the behavior of the model for signals in deep fades that has the determining effect. As the behavior of the probability density functions for amplitudes near zero differ significantly, approximations based on behavior near the mean are inappropriate.

Rician and Nakagami models have a fundamentally different density for deep fades. Modeling a Rician fading signal by a Nakagami distribution of the amplitude leads to overly optimistic results, and discrepancies can be many orders of magnitude. That is, we challenge the accuracy of the last application of the model in the above list.

Distribution of received power

A typical radio channel exhibits multipath reception, which causes fading. The mathematical evaluation of this paper addresses narrowband systems, in which the channel transfer function is sufficiently constant over the signal bandwidth. This corresponds to the assumption that Intersymbol Interference does not play a major role in the performance of the radio links. However, the models also play a role in wideband systems, in which each resolvable bin of reflected waves can be modeled to exhibit flat fading.

Rice

Rician fading assumes a dominant line-of-sight component and a large set of i.i.d. reflected waves. Reflected waves arrive with a random phase offset and the accumulation can be modeled as a phasor addition of signals with random amplitude and phase. This assumption leads to a Gaussian Inphase and Quadrature component, and a corresponding Rician amplitude. It has been shown that the instantaneous power p_i received from the i-th user, with p_i= r_i²/2 and r_i the signal amplitude, has the probability density function (pdf)

where the Rician K-factor is defined as the ratio of the power in the dominant component and the scattered (multipath) power, is the total local-mean power in the dominant and scattered waves, and I₀(.) denotes the modified Bessel function of the first kind and order zero.

Nakagami

For Nakagami fading, the instantaneous power has the gamma pdf

where G(m) is the gamma function, with G(m + 1) = m! for integer shape factors m. The mean value is . In the special case that m = 1, Rayleigh fading is recovered, while for larger m the spread of the signal strength is less, and the pdf converges to a delta function for increasing m.

In the special case that the dominant component is zero (K = 0) or m = 1, Rayleigh fading occurs, with an exponentially distributed power, viz.,

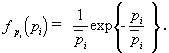
The Nakagami model is sometimes used to approximate the pdf of the power of a Rician fading signal. Matching the first and second moments of the Rician and Nakagami pdfs gives

which tends to m = K/2 for large K.

For Rician fading, the probability distribution at small powers is

For Nakagami fading, we have

Here denotes the probability that p_i < p_th .

The results are strikingly different for m larger than one. As the relation between K and m was based merely on the first and second moments, it is likely to be most accurate for values close to the mean. Outage probabilities however highly depend on the tail of the pdf for small power of the wanted signal. The probability of deep fades (small p_i) differs for these two models, so an approximation the pdf of a Rician-fading wanted signal by a Nakagami pdf can be highly inaccurate: Results differ even in first-order behavior. For Rician fading, the slope of the outage probability versus C/I is the same as for Rayleigh fading. For Nakagami fading, the slope is steeper, similar to that of m-branch diversity reception of a Rayleigh fading signal.

Method for Link Evaluation

The nakagami approximation appeared less suitable to approximate a Rician channel. Nevertheless other methods are available to make reasonable approximations in numerical evaluations of the outage probability in interference-limited situations, while restricting the complexity of calculations.

JPL's Wireless Communication Reference Website

Chapter: Wireless Channels Section: Multipath Fading, Nakagami fading