
Fade Duration
The mobile Rayleigh or Rician radio channel
is characterized by rapidly changing channel characteristics. As the amplitude of a signal received over such a channel also fluctuates, the receiver will experience periods during which the signal
can not be recovered reliably.
If a certain minimum (threshold) signal level is needed for acceptable communication performance, the received signal will experience periods of
- sufficient signal strength or "non-fade intervals", during which the
receiver can work reliably and at low bit error rate
- insufficient signal strength or "fades", during which the bit error rate
inevitably is close to one half (randomly guessing ones and zeros) and the receiver
may even fall out of lock.
This two-state simplification of the wireless channel behavior is called a Gilbert-Elliot
model.
| |
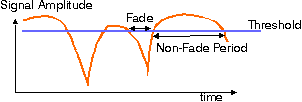 |
Figure: fade and non-fade periods for a sample of a fading signal.
|
It is of critical importance to the performance of digital mobile networks that the
block length or
packet duration is chosen taking into account the expected duration of fades and non-fade intervals.
One of two approaches can taken:
- make the block length at least an order of magnitude longer than the average fade / non-fade period, and rely on error correction to cope with burst errors.
This approach can be used for mobile reception of digital broadcast signals (e.g. DAB), particularly if the effect of fading is mitigated through
using a wide transmission bandwidth and appropriate signal processing.
This approach would be impractical in indoor office communication (wireless LANs) with high bit rates
and extremely small Doppler spreads, i.e., with very long fade / non-fade periods.
- make the block length shorter than the average fade / non-fade period
and retransmit lost data. This approach works best in full duplex mobile data systems
and random access data systems. The effective throughput depends on two aspects: 1) the probability that a block runs into a fade and 2) the overhead bits required in block headers.
If the data block length
is larger than the average non-fade period, almost all blocks
will experience a signal fade and a corresponding burst of bit errors.
This may result in an excessive packet dropping rate, unless powerful
error correction codes are used.
If the system supports a feedback signal with acknowledgments of
received blocks, it is mostly advantageous to use only limited error correction coding, but to rely on retransmission of lost blocks. To minimize the number of
retransmissions, one should choose the block length shorter than the
average fade and non-fade period.
Average Fade Duration
We use:
Outage Probability = Average number of fades per second * Average fade duration
where the average number of fades per second is called the threshold crossing rate.
Expressions for Average (Non-) Fade Duration
In a Rayleigh fading channel with fade margin M,
the average nonfade duration (ANFD) is
| |
Ö(M)
ANFD = _________
Ö(2p)fD
|
| 
|
where fD is the Doppler spread,
M is the ratio of the local-mean signal power and the minimum (threshold) power needed for reliable communication.
| |
|
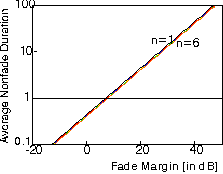
Average non-fade duration in Rayleigh-fading channel
versus fade margin for n = 1, 2, 3, 4, 5 and 6 Rayleigh-fading interfering signals.
Normalized by dividing by the Doppler Spread.
|
|
The curve for n = 6 closely resembles the curve the ANFD in an
interference-free but noise-limited channel.
Thus
- The ANFD is inversely proportional to the speed of the mobile user. Channel fading occurs mainly because the user moves. If the user is stationary almost no time variations of the channel occur (except if reflecting elements in the environment move)
- The ANFD increases proportional with the square root of the fade margin.
- The non-fade duration is not so sensitive to whether the signal experiences fades below a
constant noise-floor or a fading interfering signal.
Calculation of the distribution of non-fade periods is tedious, but has been elaborated by Rice. Because of the shape of the Doppler spectrum, fade durations that coincide
with a motion of about half a wavelength are
relatively frequent.
 Exercise
Exercise
A subscriber of an analog NMT cellular system (900 MHz)
connects a 1200 bit/s modem to his cellular phone.
He drives his car at 36 km/h. The signal experiences
wide-sense stationary noise.
Experiment with the Javascript
embedded calculator
to find the fade margin required to
ensure an average nonfade duration enough to
pass 600 bits uninterrupted.
Answer
The average fade duration (AFD) is
| |
Ö(M)
AFD = -------------- [ exp{ 1/M} -1]
Ö(2p) fD
|
| 
|
Thus
- The AFD is inversely proportional to the speed of the mobile user.
- The fade durations rapidly reduce with increasing fade margin, but the time between fades increases much slower.
| |
|
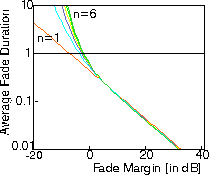
Average fade duration in Rayleigh-fading channel
versus fade margin for n = 1, 2, 3, 4, 5 and 6 Rayleigh-fading interfering signals.
Normalized by dividing by the Doppler Spread.
|
|
Experiments revealed that at large fade margins, the fade durations are approximately
exponentially distributed around their mean value.
For deep fades, Rice showed that for Rayleigh fading, the probability that
a fade duration t lasts longer than T seconds
tends to
AFD 2 AFD2 2 AFD2
P(t > T) = 2 ---- I1 [------] exp[- --------]
T pT2 pT2
where I1 is the modified Bessel function of the first kind. For small
z, I1(z) approximates z/2.
How do systems avoid long fades when the user
is stationary?














