JPL's Wireless Communication Reference Website

Chapter: Wireless Channels
Section: Multipath Fading, Nakagami fading

Distribution of received power

For Nakagami fading, the instantaneous power has the gamma pdf

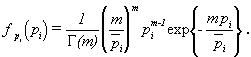
where G(m) is the gamma function, with G(m + 1) = m! for integer shape factors m. The mean value is . In the special case that m = 1, Rayleigh fading is recovered, while for larger m the spread of the signal strength is less, and the pdf converges to a delta function for increasing m.

Special case: Rayleigh fading

In the special case that the dominant component is zero (K = 0) or m = 1, Rayleigh fading occurs, with an exponentially distributed power, viz.,

Fade probability

Expressions for the distribution of signal power can be used to calculate the probability on a signal outage.

Limiting case

For sufficiently strong average signal powers, we can approximate the probability that the signal power drops below a certain threshold. We have

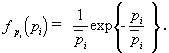
Here denotes the probability that pi < pth. Note that outage events vanish with the m-th power of the thresholds. This explains that (MRC) diversity effectively improves the performance of a radio link.

Series expansion

We define the fade margin h of a radio link as the ratio of the average received power over the threshold (i.e., the minimum required power for reliable communication), thus . The outage probability in a Nakagami fading channel can be expressed as

Exercise

Derive the above expression.



JPL's Wireless Communication Reference Website © 1999.