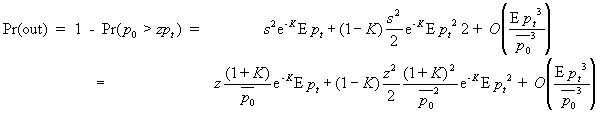Method for Link Evaluation

We address the problem of how to make reasonable approximations of the outage probability in numerical evaluations of interference-limited cellular radio systems, while restricting the complexity of calculations. The method is useful for Rician, Nakagami and Rayleigh channels.

C/I Threshold

In typical studies on outage probabilities, one defines an "outage" to occur if the signal-to-noise-plus-interference ratio drops below a certain minimum threshold value z. For instance for GSM, experiments and measurements revealed that a C/I of at least 9.5 dB is required. At lower C/I ratios, excessive burst errors occurs, synchronization acquisition becomes problematic, equalizer convergence is hampered, etc. We denote the threshold ratio as z.

The derivation

The probability that the wanted signal power p₀ sufficiently exceeds the joint interference plus noise power p_t is

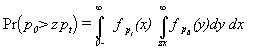
where we insert the appropriate pdf of received wanted signal power and interfering signal power . These pdfs can for instance be derived from a Rician, Nakagami or Rayleigh distribution.

The joint interference signal p_t is the sum of the powers of each individual interfering signals. For independent fading and independently modulated signals, the pdf of the joint interference power is the convolution of the pdf of individual interference powers.

In the special case of a Rayleigh-fading wanted signal, the integral over y can be solved analytically: Inserting the exponentially distribution of wanted signal power, we get

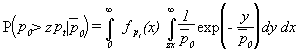
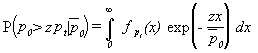
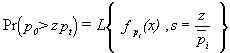
So, after solving the integral over y,

An elegant mathematical framework has been developed by interpreting the result as a Laplace transform of the pdf of joint interference power: for a wanted signal subject to Rayleigh fading, this probability can be expressed in the form

where L{f,s} denotes the one-sided Laplace transform of the function f at the point s.

SPEC	A special purposed embedded calculator (SPEC or spreadsheet) is available that evaluates the outage probability in a Rayleigh fading cellular channel, with path loss and shadowing. It also considers interference, man-made and AWG noise and delayed self interference.

Rician channel

This approach can be applied to a Rician-fading wanted signal, using the series expansion

for the modified Bessel function I₀. This gives

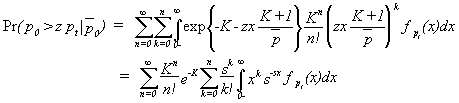
Using the properties of the Laplace Transform, this can be written as

Nakagami channel

Inserting the gamma pdf, one obtains

Generic Method

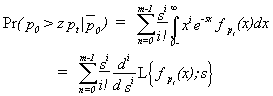
For both models, this probability can be expressed in the same (generalized) form

Table 1 gives the appropriate coefficients a_i and argument s₀for various propagation models.

Table 1: coefficients a_i and argument s₀ for link success probability

Computational Method

The probability of a signal outage at signal-to-interference ratios sufficiently above 0 dB ( ₀ >> Ep_t ) is found from the behavior of the Laplace expression at small values for s. We expanding the Laplace transform into the McLaurin series

For Nakagami fading with integer m, this is gives the outage probability

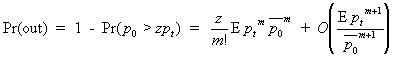
For Rician fading, we find

JPL's Wireless Communication Reference Website

Chapter: Wireless Channels Section: Multipath Fading, Nakagami fading