PDF of received signal amplitude
In order to obtain the probability density function
(PDF) of the signal amplitude r
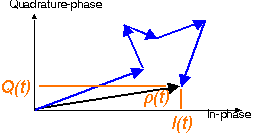
of a Rayleigh fading signal, we observe the random processes of the inphase and quadrature components, I(t) and Q(t) , respectively, at one particular instant t0.
| |
|
Received signal (in black) consisting of N = 5 reflected waves (in blue).
The resulting signal amplitude r
consists of an inphase component I and a quadrature component Q.
If the antenna moves the relative phases of the reflected waves
change over time, so r, I and Q
become a function of time t.
|
|
If the number of received waves N becomes very large and all are independent and identically distributed (i.i.d.), the central limit theorem says that I(t0) and Q(t0) are (zero-mean) Gaussian random variables, each with variance
s2.
Lord Rayleigh argued in 1889 that the received signal
r(t) = r(t) cos (2p fct + q(t))
has a Rayleigh amplitude
r(t) which is found from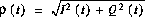 
,
and a uniform phase
q(t)
between 0 and 2p. The probability density of the amplitude is described by the
"Rayleigh" pdf
r r2
fr(r) = --- exp(- ----)
s2 2s2
for r > 0. This result will be derived in the following exercise, with worked solution. An important application of a probability density function
is the calculation of outage probabilities, that is the probability that the signal strength drops below a certain threshold level.
Exercise
Let the complex random variable z = x + jy with x and y i.i.d. Gaussian with zero mean and variance s2. Here j denotes SQRT(-1).
Note that x and y correspond to
the inphase and quadrature components of a Rayleigh fading signal, respectively.
We interpret this as x = I(t) and y = Q(t) , respectively, at one particular instant t.
- Show that the amplitude r (r= |x|) is Rayleigh distributed.
Hint
Answer
- Show that the expected value Er = SQRT(p/2)s, thus about 1.2533 times the standard deviation s.
- Show that the local mean power
Er2/2 = s2.
- Show that the variance of the amplitude equals s2
(4 - p)/2.
Simulations have shown that the Rayleigh pdf appropriately describes the fading of the amplitude if N is larger than 6. Measurements over non-line-of-sight paths at UHF frequencies in urban environments confirmed the accuracy of the Rayleigh pdf.
PDF of Received Power
The instantaneous power p, with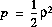 
,
thus, averaged over one RF-cycle, has the exponential pdf
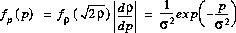
where s2
is the local-mean power.
Exercise
Find the cumulative distribution of the received power. In a cellular voice channel, a signal outage occurs if the instantaneous signal-to-noise ratio is less than z = 10 (10 dB). Find the required local-mean power to ensure an outage probability of less than 1%. Find the corresponding fade margin, defined as the excess power above the threshold zN with N the noise power, and z the minimum tolerable signal-to-noise ratio.
Exercise
Write a computer program that plots the probability that a Rayleigh fading signal drops below a certain threshold. Show that the curve can be plotted as a
function of a fade margin, i.e., the ratio between the local mean power
and the threshold.
If the receiver can choose between L (L= 1,2, ..)
different antennas and each antenna sees an independently fading signal, how does this improve the probability? (Hint: see diversity)
Solution.
If the set of reflected waves are dominated by one strong component, Rician fading is a more appropriate model.
