Throughput of ALOHA Networks
To express the throughput of the ALOHA random access scheme, it is often assumed that message transmission attempts occur according to a Poisson process with rate G attempts per slot. For channels in which
a transmission is successful if and and only if in that slot
only a single packet transmission is present, the throughput of successful
messages is equal to
- The probability of having just one message: S = G exp{-G},
or equivalently,
- The attempted traffic G multiplied by the probability exp{-G}
that no interfering message is present
Both arguments yield the well-known result for the throughput of slotted ALOHA:
S = G exp{-G}
For unslotted ALOHA without capture, a test packet is destroyed by any overlapping transmission starting in the time window that
- starts one packet time before the transmission of the test packet and
- closes at the end of the transmission of the test packet.
Hence, packets transmitted over an unslotted ALOHA channel see on average
twice as many interfering packets as in slotted ALOHA. In fact
S = G exp{-2 G}
Both unslotted and slotted ALOHA exhibit the typical behaviour that
- at low traffic (small G), S is approximately equal to G
- at high traffic loads (large G), S decreases to zero. Almost all packets
are lost in collisions.
- one throughput value S corresponds to two values of G. The curves misleading suggest that one
G would be stable while the other is unstable. For systems without capture it turns out, however, that the ALOHA system with
a fixed retransmission procedure, independent of the history of the network, is always unstable.
ALOHA in Mobile Radio Nets
In a radio channel, packets may be received successfully
despite interference from competing terminals. This is called `receiver capture'.
The larger the differences in received signal power, the more likely it is that one signal is sufficiently strong
to capture the receiver
The throughput becomes G times the probability that a particular (a priori chosen) packet is
sufficiently stronger
than the sum of all interfering packets.
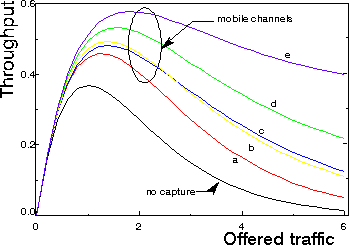
Figure: Throughput S of Slotted ALOHA network (in packet per time slot)
versus the attempted traffic G.
- Without capture; any collision destroys all packets involved
- With Capture (receiver threshold is 4)
- a: Rayleigh fading only
- c: Shadowing and Rayleigh fading
- e: Near far effect and Rayleigh fading, Uniform distribution of terminal is a circular cell around the receiver.
- b,d: Some other capture models
Note that some capture models do not predict that S reduces to zero for large G.
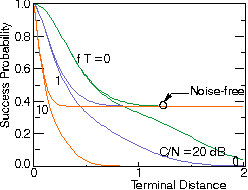
Figure: Probability that an access attempt is successful
versus the distance between terminal and base station.
- Average message arrival and retransmission rate: 1 packet per unit of time.
- Terminals
quasi-uniformly distributed over cell, with cell boundary approximately at unity distance.
- Receiver threshold 6 dB.
- Plane earth loss (40 log d)
and narrowband Rayleigh fading.
- Various packet durations T, normalized to the Doppler spread.
- Median signal-to-noise ratio (for user at distance 0.734)
is 20 dB.
- New arrivals and retransmissions for a stationary Poisson process. The network is stable. Theoretically, this condition can only
be satisfied if the retransmission backoff delay is infinitely large.
Computation of Throughput
The throughput S is found as the offered traffic, multiplied by the probability that a particular,
a priori chosen test packet captures
the receiver. Thus
inf
S = G sum Prob(capture |i interferers) Prob ( i interferers)
i = 0
where the probability on i interferers is Poissonian with value G.
The capture probability equals one minus the outage
probability.
In most analyses, the probability of capture is first expressed for a given local mean power of the test signal.
In a Rayleigh-fading channel, the probability of receiving a signal with local-mean power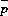 
_0
can be expressed in terms of Laplace Transforms
of the probability density functions of the power p_i of interferer i. That is,
^i ^i z
P(capt | i) = Prob(capt|i=1) = Laplace {p_i ; ---}
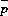_0
where z is the capture ratio or receiver threshold.
This observation leads to the mathematically convenient definition of
the interference-vulnerability weight function.
Throughput for various propagation and traffic distribution models
One can use the above expression to find the throughput for various distributions
of terminals over the "service" area.
- Ring model.
For mathematical simplicity, initially the throughput of ALOHA network
was computed for the special case that all user signals are received with the same mean power.
This model is also appropriate for
DS-CDMA packet networks with power control.
Delay and throughput performance of packet
can be optimized choosing the appropriate
spread factor and retransmission strategy.
- Uniform distribution of packet transmissions
- Uniform within a circular cell
- Uniform with infinite extension
.
This model is appropriate for
- Collecting telemetric data in ISM bands.
- Collecting road-traffic data from probe vehicles. Floating Car Data.
- Cellular ALOHA networks with frequency reuse; Virtual Cellular Networks (VCN)
Random access network with stack collision resolution and DS-CDMA
- Uniform throughput.
This implies that users at remote locations have to perform more retransmission attempts. It results in non-uniform attempted traffic.
- ALOHA messages generated by (probe) vehicles participating in road traffic, considering a specific
road infrastructure.
The expressions for capture probabilities can also be used to find the network delay
and stability.
