JPL's Wireless Communication Reference Website

Chapter: Data Networks
Section: Random Access, ALOHA

Dynamic queueing behavior of ALOHA Nets

In an ALOHA network, data packets experience delays because of a number of queuing mechanisms. Here we address the delay caused by the fact that packets unsuccessfully offered to the random access channel have to be retransmitted after a random waiting time.

In a simplified analysis of throughput S and the probability of success it is often assumed that unsuccessful packets are rescheduled, so that each new attempt is seen as a new contribution to the offered traffic G, which is independent of the history of packet arrivals and collisions.
More accurate analyses address a queueing model based on a Markov Chain. This model offers the possibility to evaluate the effect that after an unsuccessful transmission attempt, the terminal retransmits the packet with a short random waiting time to reduce the delay. If multiple terminal have packets for retransmission, destructive collisions may continue to collide. The backlog, packet delay and also the stability of the network are studied from such a Markov Chain.

This page addresses the latter model.

Terminal Model

A well-known procedure for evaluation of the stability of the ALOHA channel considers a finite or infinite population of N terminals. For the case of a finite population an additional assumption is that each terminal has a buffer of length one to store the last packet, which may need retransmission. No new packets arrives in the same terminal as long a one packet is waiting for retransmission. The local behaviour of such a terminal is modelled by a tri-state Markov chain.

In the origination state (O), a packet is generated (for transmission in the next available time slot) with probability P₀.
In the transmission state (T), the terminal is busy with either transmitting a new packet or retransmitting a collided packet. The mobile terminal returns to the O-state if it receives a positive acknowledgement at the end of the time slot during which a packet is transmitted; otherwise it enters the retransmission or 'backlogged' state (R).
From the latter state, retransmission (i.e., transition into the T-state) occurs with probability P_r. A backlogged terminal is blocked in the sense that no new messages can arrive when the terminal is in state R.

This tri-state model implies the absence of a buffer for more than one packet in a mobile terminal.

Network Model

The global behaviour of the entire slotted ALOHA network is also modelled by means of a finite or infinite Markov chain. The state of the network represents the number of terminals m in the state R at the start of the time slot. This is also called the system 'backlog'. With a population of N terminals, we have N + 1 states. During a time slot, i (i = j + k) packets are transmitted whenever j terminals in the O state and k terminals in the R-state change into the T-state at the same time. The probability of a transition into another state may be obtained from the probability distribution of j and k and the capture probability C_j+k that one of the j + k packets survives the collision. Here, k is a binomial random variable. For an infinite population j is Poisson, in a finite population j is binomial. For a given backlog, j and k are independent.

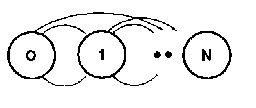
Figure: Markov model for number of terminals in backlog. Population size N.

Exercise

Explain why the transition from zero backlog to one terminal in backlog can occur in mobile channels with capture but is unlikely to occur in LANs using a wired ALOHA channel, thus without capture.

Calculations based on the above Markov model take into account that the system backlog m and the probability of successful transmission are statistically correlated: With a high system backlog, frequent retransmissions occur (if P_r > P₀), and collisions are very likely. Hence, the probability of success generally reduces with increasing system backlog (if C_k < C_m for k > m), which may lead to saturation or instability of the network if terminals in backlog employ (too) short retransmission waiting times (too high P_r). If the number of terminals N is finite, the network may become bi-stable, i.e., the network oscillates between low and high backlog states.

Dynamic behaviour

The throughput S_m in state m: is found from the probability of successfully transmitting a packet in a time slot, and is determined by averaging the probability of i (i = j + k) colliding packets, given a backlog of m terminals, i.e.
Stability: is studied from the expected drift in each state, defined as the difference between the expected 'input' traffic (N - m) P₀ and the expected 'output' traffic S_m in that state, and is expressed in states per time slot.
The average total network throughput S: is found by averaging S_m over the state probabilities m. In such analysis, the state probabilities (that the network is in state m (m = 0, 1, ... , N)) can be obtained recursively from the transition probabilities.

Useful Properties and Theorems

In a well-functioning network in equilibrium, the channel throughput must equal the newly generated traffic

For stable (and bi-stable) systems, the access delay can then be evaluated from Little's formula:

                   average number of packets in backlog
average delay =   -------------------------------------
                                 throughput

Network Stability

The first analyses of the stability of the ALOHA network were reported by Carleial and Hellman, and by Kleinrock and Lam.

Infinite population

With an infinite population of users and a fixed retransmission back-off parameter, the ALOHA system is always unstable, unless capture occurs.

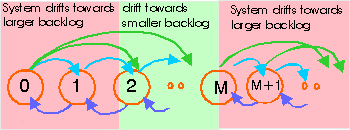
Figure: Markov model for number of packets in backlog. Backgrounds: Greenish: negative drift; reddish: positive drift

It can be shown that

With some small but non-zero probability the network enter some particular state M with M a large integer.
For an appropriately chosen M and all states with backlog larger than M, the network drifts to a higher state
Under such conditions the network is unstable

Finite population

The finite-population ALOHA system can be bistable:: the system either is in low backlog or in high backlog. Every now and then it hops from high backlog to low backlog, but it is unlikely to be in intermediate states, as it will rapidly drift away from these states.

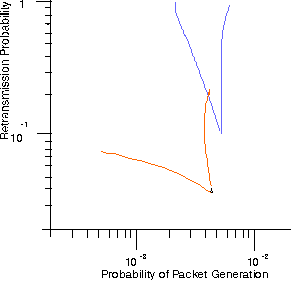Figure: Bistability area for a network with N =100 users without capture (orange) and with imperfect capture (green) (capture ratio z = 10) in mobile channels.

The above figure gives the region for P₀ and P_r where the network with 100 terminals is bistable. A conservative receiver threshold of 10 dB (z = 10) is considered, so these results may be somewhat pessimistic. The bistability area for ALOHA without capture was computed first by Onozato and Noguchi. Areas mapping the stability of a slotted ALOHA network with capture were derived for the case that the population of terminals is divided into a group transmitting at high power and a group transmitting a low power.

Van der Plas and Linnartz estimated the area of bistability by trial and error with the technique used to obtain drift curves. A uniform spatial distribution, shadowing (6 dB) and Rayleigh fading are considered. When receiver capture occurs, the mobile network exhibits bistability at substantially higher packet traffic loads, even for a pessimistic receiver threshold of 10 dB (z = 10).

It appears that the network is always stable, irrespective of the retransmission probability P_r, if P_r < P_0,max, with roughly P_0,max = 2 . 10^-3. This agrees with the observation by Ghez, Verdu and Schwartz, that for

packet arrival rates < the limit of the capture probability for collisions with infinitely many signals ,

the channel is stable if the probability of capture is independent from slot to slot. However, this may be a strong assumption if the retransmission waiting time is small. If packets are retransmitted from the same location, they are received with the same power, as the initial transmission attempt. If the same set of data packets collide again with the same powers for all signals involved, interference is likely to cause packet loss during all successive collisions.

Controlling the Retransmission back-off

See the collision resolution animation and the exercise.

Various schemes exist to ensure stability and to resolve collisions

Adaptive control of the retransmission probability
- Ad hoc approaches
- Optimal retransmission backoff
Dynamic Frame Length ALOHA
the tree algorithm and
the stack algorithm.

Near-far distribution of terminals

Several aspects of the spatial distribution of terminals are relevant to consider:

Packet transmissions are often assumed to be uniformly distributed over the coverage area. In this event, the probability of correct reception of one out of n colliding packets, has some non-zero limit for large n. This assumption may be overly optimistic.
As an alternative, other spatial distributions can considered. This allows more realistic modelling of the packet traffic very close to the central receiver. Simulations reveal that in such case, the system may suffer much more from instability effects than in the case that some signals are received with very large power.
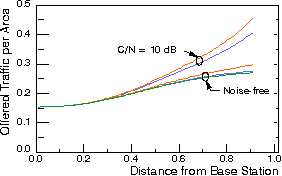
Most retransmissions originate from the boundary of the service area. Such signals are weak and easily lost in collision. This has a negative influence on stability.

Figure: Expected number of (re-) transmission attempts needed, as a function of terminal location
For details see Cellular ALOHA Networks.