JPL's Wireless Communication Reference Website

Chapter: Wireless Propagation Channels
Section: Multipath Fading, Fade Durations

 

Appropriate Choice of Packet Length

Multipath fading affects the throughput of data packets on a wireless Rayleigh-fading link:
If the rate of fading is fast, relative to the packet length, it is likely that each received packet contains burst errors.  

Example 1: Noise-Limited Rayleigh-Fading Link

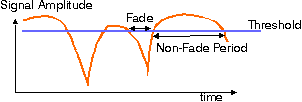 A simple model to estimate the probability of successfully receiving a data packet over a fading channel assumes that the fading is memoryless. i.e., transitions from fade to non-fade periods occur randomly without any influence of how long the channel is already in a fade or non-fade interval.

The channel state can than be modelled as a Markov chain with a fade and non-fade state. See Gilbert-Elliot model. Packet transmissions are assumed to be successful whenever the transmission starts in a non-fade interval and that non-fade interval lasts for the full duration of the transmission. The probability that the packet transmissions starts in a non-fade interval equals the outage probability and is determined by the probability that the received amplitude is sufficiently below the noise level. For Rayleigh fading, we consider the exponential probability density (PDF) of received power. Integrating the exponential PDF , from threshold value pth to infinity, 

                       pth             1
         P1 = exp (-  ----)   = exp(-  --)
                       pl              h
where h ("eta") is the fade margin (received local-mean power divided by minimum required received power).

The probability that the non-fade interval lasts for the full duration of the transmission is exponential with 

                      T
         P2 = exp (-  ----)
                      TNF
where T is the packet duration and TNF is the average non-fade duration.

The probability of successful reception is P = P1 P2, so

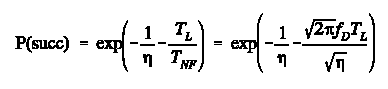
where TL is the packet duration and fD is the Doppler spread.


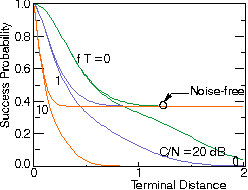
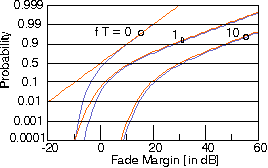Figure: Probability that a packet is received without fade in a (frequency nonselective) Rayleigh fading channel versus fade margin. Orange: single Rayleigh fading interferer, no noise. Violet: Many weak interferers or Gaussian Noise. Various data block or "packet" durations T, relative to Doppler spread f.

The effective throughput depends on the probability that a packet is received successfully and on packet overhead. The probability of being received successfully decreases with increasing packet length. This suggests that packets should be short with respect to the non-fade durations. In most systems the overhead (sync headers, addressing, error control coding, etc.) is relatively independent of the number of users bits. To reduce overhead, packets should be long. The following curve shows where the optimum length can be found.


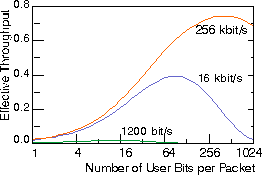
Calculate the effective throughput for your own system.

The derivation of this result is covered in the slide show.
Figure: Effective Throughput of fade-free packets in a (non-selective) Rayleigh fading channel, as a function of number of bits (48 header bits not included) in a packet for bit rates of 1200; 16k and 256 kbit/s. Doppler spread 60 Hz. Fade margin 10 dB.

Example 2: ALOHA Random Access


Figure: Probability of successful transmission in wireless data network with ALOHA random access, versus terminal location.

How to select a bit rate?

Packet length and rate of fading
Slow versus fast fading. Role of error correction

Fast bit rates ensure good throughput: Most packets are successful, but some are lost in fade. With slow transmission rates on the other hand, all packets are likely to contain one or more bursts of errors, so virtually all packets may be lost.

Note however, that with increasing bit rates, channel dispersion becomes a problem. See also: a comparison of various digital modulation methods.


JPL's Wireless Communication Reference Website © 1993, 1995.