JPL's Wireless Communication Reference Website

Chapter: Data Networks
Section: Random Access, Stack Algorithm
Also: Analog and Digital Transmission
Section: CDMA, Direct Sequence CDMA


DS-CDMA Packet Network with Random Access

In modern multi-user wireless networks, substantial effort is being made to use scarce radio spectrum resources in the most efficient way. Approaches to enhance the performance of packet-switched networks with bursty traffic typically employ advanced transmission techniques such as Code Division Multiple Access (CDMA) or advanced medium access protocols, such as the tree or stack algorithms for collision resolution. The performance of a packet radio network employing Direct Sequence (DS) Code Division Multiple Access highly depends on the spread factor.

Although bandspreading with perfectly orthogonal signals may theoretically enhance system capacity, it does not resolve the instability of ALOHA random access unless special measures are taken to control retransmission traffic. Using a Stack Algorithm at small traffic loads, the packet delay is minimized if no spreading is applied. At large traffic loads, perfect CDMA enhances performance, but for imperfect signal separation at the receiver, advantages of CDMA are lost. Typically the capacity of the Stack Algorithm can be enhanced from 0.32 to at least 0.40 if a large spreading factor with perfect signal separation is employed.

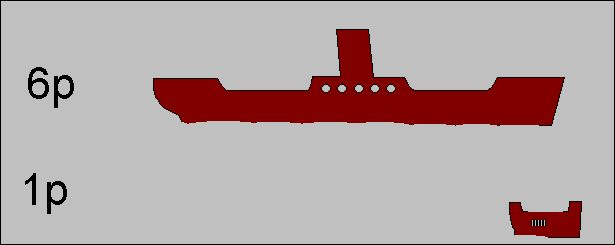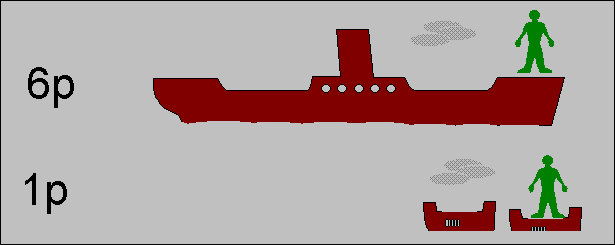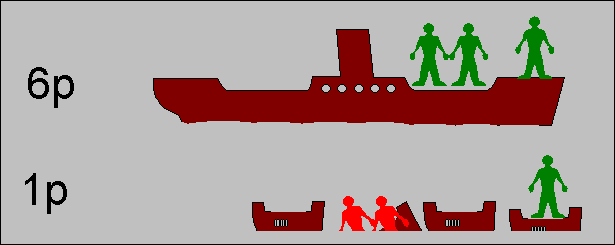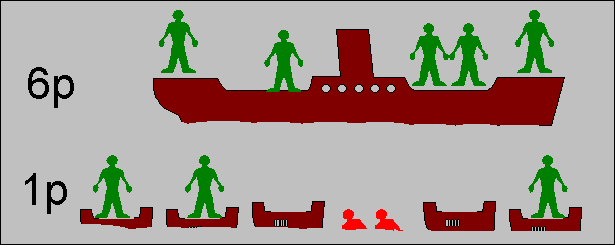
  Intuitive explanation of the effect of CDMA in a random access network, by making an analogon with randomly arriving boat passengers.  

In a lightly loaded network, the packet delay increases if one applies spread spectrum transmission. This is explained by the fact that without intentional spreading, messages can have very short duration, which substantially reduces the transmission time. On the other hand, at large traffic loads, spreading may enhance performance, provided that near-perfect detection methods are used. Presumably interference-cancellation techniques and multi-signal detection are needed to reliably separate up to C signals in a CDMA system with spreading factor C.

To some extent, these observations disagree with favorable results for CDMA cellular telephony systems. In circuit-switched telephony the main performance criterion is a guaranteed maximum outage probability for the entire duration of a call. The 'averaging' the effect of interference over time and bandwidth may then favorably affect the probability that the interference occasionally is too large. In efficient packet-switched networks however, the interference can be fairly large for a substantial portion of time without excessively affecting the average performance. In such networks, capture probabilities benefit if the interference power level fluctuates from slot to slot. Moreover, the delay penalty from longer packet transmission times due to spreading appears to be significant.

Fair Comparison: Fixed System Bandwidth

We address a multi-access channel with a large (possibly infinite) number of distributed terminals that send data packets to a central receiver. Packets arrive according to a temporal Poisson process with mean arrival rate packets per second. The fixed message length is L bits and the total system bandwidth is Bc.

For a system without spreading and modulation compactness of r bit/s/Hz, the packet duration TL is TL = L / (r Bc). The system is slotted, i.e., the time axis is divided into slots and any packet transmission starts at the beginning of a slot and finishes at the end of the same slot. Ignoring propagation delays and power-up (guard) times, we assume that the slot time is identical to TL.

We compare this system with CDMA transmission with spreading factor C . For a fair comparison we maintain the same total system bandwidth, irrespective of the spreading factor considered. This implies that the slot duration and packet transmission time are proportional to C so these become equal to TL = C L / (r BC). The message arrival rate, expressed in packets per time slot becomes TL = C L / (r Bc). We normalize the unit of time taking L / (r Bc) = 1, i.e., one unit of time equals the slot duration in a system with C =1.

CDMA Capture Model and Throughput

Optimistic Model

In ideal CDMA, one often assumes perfect reception as long as the number of packets present in the channel is less than the spread factor. Thus, in a narrowband system (C = 1), successful transmission only occurs if exactly one packet is present in that slot. If the arrival process of packets were truly Poissonian in slotted ALOHA, the throughput per unit of time becomes 
                    C-1   (CG)^k
   S = G exp(-CG)  Sum    ------
                    k=0    k!
where S denotes the expected number of successful packets per slot and G denotes the number of attempted transmissions per slot.

For C = 1, this reduces to the throughput of slotted ALOHA without capture: S = G exp(-G). Increasing C adds more terms, so it enhance the throughput.

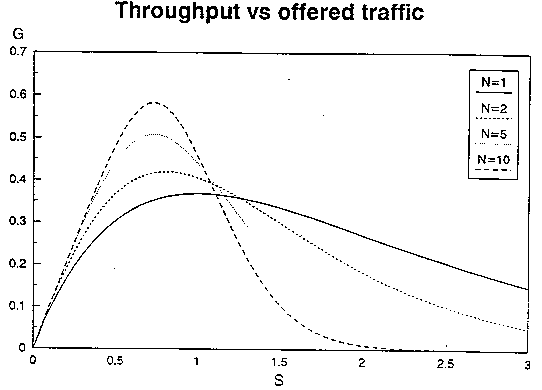
Throughput improves with increasing spread factors: S tends to G (S goes to C , G goes to C ) for less than unity and C goes to infinity.

If one uses retransmission probability p, and assumes a steady-state stable network, the delay d can be expressed as 

           TL      G  exp(-CG) 
     d =   ---   ----------------  
            p       C-1   (CG)^k
                   Sum    ------
                    k=0    k!

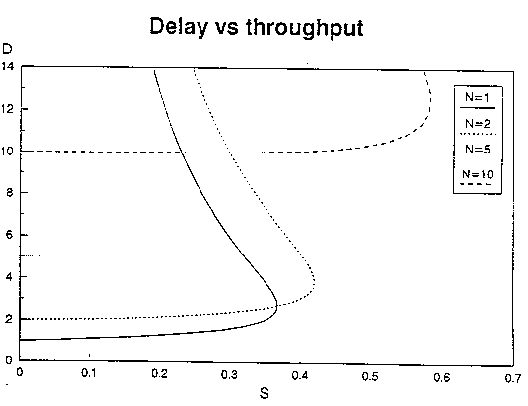
This suggests that with increasing C, the ALOHA random access system 'looses' its contention character and its properties become closer to that of a fixed assignment scheme.

Pessimistic Model

A typical correlation receiver attenuates CDMA interference by a factor C. We assume that all signals are transmitted over a Linear Time-Invariant (LTI) frequency non-selective Additive White Gaussian Noise (AWGN) channel. The energy per bit is taken identical and constant for all users and it is denoted as Eb. The noise spectral power density is N0. The signal to noise ratio is Eb/N0. A commonly used model for the bit error rate given K interferers is to assume that interfering CDMA signals behave a AWGN, but attenuated by the spread factor C. We assume that all signal are received with the same signal power. This allows us to compute the probability of not more than t errors in a packet. The number of packets k out of K colliding packets capture the receiver has a binomial probability distribution.

Maximum Throughput

The maximum arrival rate cr of new messages that gives a stable operation of the stack algorithm is summarized below.
Spread Factor Perfect CDMA
Imperfect CDMA
t = 0 t = 2
cr cr cr
C = 1 0.32 0.32 0.32
C = 2 0.34 0.16 0.18
C = 5 0.37 0.13 0.17
C = 10 0.40 0.12 0.15
C = 15 0.40 0.11 0.15
C = 20 0.40 0.10 0.14

CDMA-ALOHA is Unstable

Despite these seemingly beneficial effects on throughput, even perfect CDMA with finite C cannot repair the instability of the ALOHA system with a fixed retransmission back-off probability. Even though the probability on a destructive collision involving more than C new packets rapidly becomes small with increasing C, retransmission traffic spoils the stability of networks. The proof is based on the observation that for any finite C and fixed retransmission probability p, their exists an M such that if more than M terminals are in backlog, the backlog is expected to grow without bounds. As the probability of having M terminals in backlog is nonzero, the system will eventually experience ever-increasing backlog. In order to ensure reliable operation, CDMA packet networks thus need a control mechanism that regulates the number of packets transmitted in each time slot.

Efficient collision resolution algorithms have been proposed, such as the Stack Algorithm. For this system the network is stable, even if the number of terminals in infinite. Hence, for the stack algorithm one can compute delays, whereas rigid computations show that the delay in infinite-user ALOHA nets is unbounded.

Packet Delay

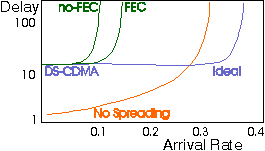
  Figure: Delay for stack random-access scheme, normalized to slot duration of system without spreading. Arrival rate in packets per time slot, for a system without spreading.
Signal to noise ratio (Eb/N0) = 100 (20 dB).
Packet length 256 bits.
Orange: no spreading.
Violet, Green: CDMA with 10 dB spreading gain: perfect signal separation; without error correction; and with two-error correcting code. 		 
The above figure has been obtained for packets of L= 256 bits without error correction coding (t = 0) and with a two-bit error correcting code (t = 2). The arrival rate corresponds to the expected number of new packets per slot in an non-spreading system. The message delay expressed in seconds is [3/2 + d] C, so it includes one packet time and a half for the random waiting time till the beginning of the next slot and the message transmission duration.

The curves show that C = 1 gives a significantly smaller delay than a larger spreading factor. For large , however, spreading gives better performance.
Even if CDMA allows perfect capture, for l < 0.3 the delay is minimized if C = 1.



JPL's Wireless Communication Reference Website © Jean-Paul M.G. Linnartz and N.D. Vvedenskaya, 1993, 1995.