|
JPL's Wireless Communication Reference WebsiteChapter: Data Networks
|
Q(r) = exp (-G)where G is total attempted packet transmission traffic on the channel. This does not depend on the distance r between the terminal transmitting the packet and the receiver.
In a radio channel with capture, not all present
packets cause harmful interference. So the effective interfering
traffic load may be much less than G.
Because of propagation path losses,
transmissions from nearby terminals will be less vulnerable than
packets from remote terminals.
We define G(r) as the average number of packets
transmitted per slot, per unit of area, from a distance r.
Vulnerability Circle: a postulated model
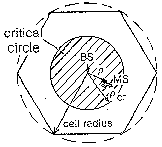Abramson suggested in 1977 to consider interference to be harmful if and only
if it arrives from terminals closer to the base station than
c r with c a system and propagation constant and r the propagation
distance for the test packet.
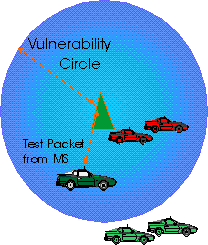Thus,
cr
Q(r) = exp (- int G(x) x dx)
x =0
This model ignores channel fading, shadowing and cumulation of
interference if multiple packets collide.
inf
Q(r) = exp (- int W(r,x) G(x) x dx)
x =0
where the weight function is of the form
z r^b
W(r,x) = -----------------
z r^b + x^b
where
If the interfering signals also exhibit shadowing, a weight function also exists.
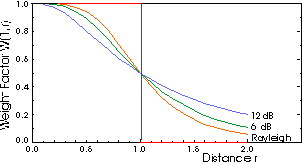
Figure: Weight function W(1,x)
