JPL's Wireless Communication Reference Website

Chapter: Wireless Channels. Section: Multipath fading; Rayleigh fading.

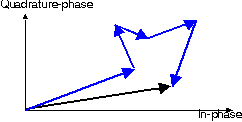Figure: Phasor diagram of a set of scattered waves (in blue), resulting in a Rayleigh-fading envelope (in black)

We address a large set of reflected waves. Let the n-th reflected wave with amplitude c_n and phase f_n arrive from an angle a_n relative to the direction of the motion of the antenna.

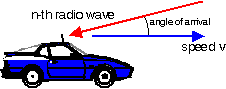
If the mobile antenna moves a small distance e, the n-th incident wave, arriving from the angle a_n with respect to the instantaneous direction of motion, experiences a phase shift of

  2p  e
  -----  cos(an)
    l

Thus all waves experience their own phase rotation. The resulting vector may significantly change in amplitude if individual components undergo different phase shifts.

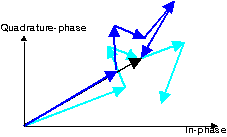Java animation

Figure: Phasor diagram of a set of scattered waves after antenna displacement (in blue) and before motion (in light blue), resulting in a Rayleigh-fading envelope (in black)

In mobile radio channels with high terminal speeds, such changes occur rapidly. Rayleigh fading then causes the signal amplitude and phase to fluctuate rapidly.

If e is in the order of half a wave length (l/2) or more, the phases of all incident waves become mutually uncorrelated, thus also the amplitude of the total received signal becomes uncorrelated with the amplitude at the point of departure.

Doppler Shifts

Autocovariance

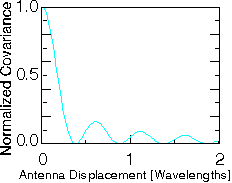
The normalised covariance L(e) of the electric field strength for an antenna displacement e is of the form

          2    2p e
L(e)  =  J   (-----)
          0     l

with J₀(.) the zero-order Bessel function of the first kind.
The signal remains almost entirely correlated for a small displacement, say e< l/8, but becomes rapidly independent for larger displacements, say for e > l /2.

Figure: Auto-covariance L(e) of the electric field strength in a Rayleigh-fading channel versus the normalised antenna displacement e/ l (or T fm) in horizontal direction.

The antenna displacement can also be expressed in the terminal velocity v and the time difference T between the two samples (e = v T). So with f_m the maximum Doppler shift (f_m = v f_c / c).

How do systems handle fast multipath fading?

JPL's Wireless Communication Reference Website © Jean-Paul M.G. Linnartz, 1993, 1995.