
 |
JPL's Wireless Communication Reference WebsiteChapter: Wireless Channels
|
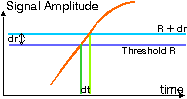
Figure: Threshold crossing. Threshold R is crossed with derivative dr/dt.
The above crossing of the threshold R with width dr lasts for dt seconds. The derivative of the signal amplitude, with respect to time, is dr / dt.
If the signal always crosses the threshold with the same derivative, then:
Average number of crossings per second * dt = Probability that the amplitude is in the interval [R, R + dr].
The probability that the signal amplitude is within the window [R, R + dr] is known from the probability density of the signal amplitude, which can for instance be Rayleigh, Rician or Nakagami. Moreover, the joint pdf of signal amplitude and its derivative can be found. For a Rayleigh-fading signal.
var = 2 * p2 * (Doppler spread)2 * local-mean power
The expected number of crossings per second is found by integrating over all possible derivatives.
SQRT(2 p)fD
TCR = -------------- exp{ -1/M}
SQRT(M)
| 
|
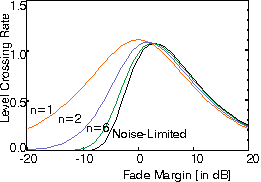
Threshold Crossing Rate in Rayleigh-fading channel
versus fade duration for n = 1, 2, and 6 Rayleigh-fading interfering signals
and for a constant noise floor.
Normalized to the Doppler Spread.
The TCR curve has a maximum if the local-mean-power is about as large as the threshold noise or interference power. If the signal is on average much stronger than the threshold, the number of threshold crossings (i.e., deep fades) is relatively small. Also, if the signal is much weaker than the threshold, the number of crossings is small because signal "up-fades" are unlikely.