Drift of Backlog in ALOHA network

Investigation of the stability of an ALOHA network requires us to address the expected drift d_m in each state. The state of system is the number of terminals that are in backlog, i.e., the number of terminals that will soon attempt a retransmission of previously unsuccessful packet.

Drift: is defined as the difference between the expected 'input' traffic (new packet arrivals but not retransmissions) and the expected 'output' traffic (or 'throughput') in that state. The drift is expressed in states per time slot.

This drift can be interpreted as the average motion towards another (higher or lower) state, when the network is in state m. The network is expected to operate in a state near an equilibrium point, i.e., where the expected drift crosses zero with negative derivative.

Drift Analyses

The first analyses of drifts and the stability of the ALOHA network were reported by Carleial and Hellman, and by Kleinrock and Lam.

Infinite population

With an infinite population of users and a fixed retransmission back-off parameter, the ALOHA system is always unstable, unless capture occurs.

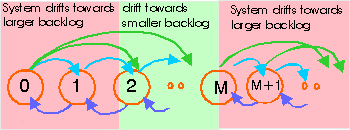
Figure: Markov model for number of packets in backlog. Backgrounds: Greenish: negative drift; reddish: positive drift

For many ALOHA networks, the state space can be divided into three groups of states

States with small backlog and positive drift
States with moderate backlog and negative drift
States with high backlog and positive drift.

For the ALOHA system, it can be shown that a finite M exists such that the drift is positive for all states larger than M. Intuitively this is clear: the more terminals in backlog (high state), the more signals will be involved in each collision, the smaller the probability of capture. In systems without capture such M exists for any arrival rate of new packets, no matter how small.

Pake's Lemma says that all states in the system must be transient if the drift is positive for all states beyond a finite M. This lemma thus says that eventually the system will drift away into larger and larger backlog, never to return to states with reasonable small backlog.

Finite population

With a finite population, the system can not drift away to ever growing backlog, as it can occur for a system with an infinite number of terminals. Nonetheless, the system can exhibit bi-stability. The system then oscillates between periods of being in low backlog and periods with high backlog. The number of terminals, the message arrival probability, the retransmission probability and the capture performance all have a substantial effect of the drift and stability. (

See also: terminal model in the stability page.)

Neither Carleial and Hellman nor Kleinrock and Lam considered capture in their papers. Namislo reported drifts, stability and delays for a network with capture. The probabilities of capture were obtained from Monte-Carlo simulation, taking account of path losses; fading and shadowing were not considered. Van der Plas and Linnartz included the effects of Rayleigh fading and shadowing and derived capture probabilities analytically.

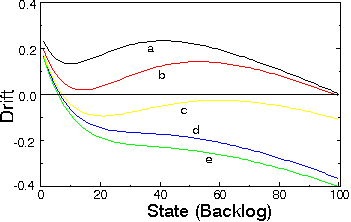
Figure: Drift for a network of 100 users for a receiver without capture (a), and for a receiver with threshold of 6 dB (z = 4) for

a channel Rayleigh fading only (b),

shadowing (6 dB) and Rayleigh fading (c),

near-far effect and Rayleigh fading (d),

near-far effect, 6 dB shadowing and Rayleigh fading (e).

Exercise:
In the above figure, indicate in (or near) which state(s) the network most likely is. answer

Discussion

The drift at high backlog is mainly determined by the probability of capture realised in the event of many colliding terminals.

In a Rayleigh-fading channel with identical local-mean power for all users, the probability that one out the many Rayleigh-fading signals is sufficiently stronger than the joint interference is low, as compared to other propagation mechanisms. Consequently, the drift from full saturation is almost zero in curve (b).
The log-normal distribution, due to shadowing, exhibits a higher probability of upfades of the signal power, resulting in a negative drift, away from the situation with all terminals in backlog.
The uniform spatial distribution, has a fast recovery from states with high backlog. This is due to terminals that are very close to the receiving base station. Packets from such terminals have capture probabilities close to unity, irrespective of the number of contenders. In this event, the drift near full near saturation and the throughput roughly equal the capture probability for collisions of many packets, which is almost constant for collisions of many signals.

Simulations indicate that reducing the probability of retransmission (large back-off time) has a positive effect on the network performance in saturated networks (increasing throughput, decreasing backlog and delay), but a negative effect in stable, unsaturated networks (lower throughput, increasing backlog and delay). In bistable nets, appropriate enlargement of the back-off time can remove bistability, but this measure may not sufficiently relieve the backlog and packet delay: The curve suggests that a relatively drastic reduction of transmission probability may be required. Reducing this in a bistable network can result in a stable network, but with relatively high backlog.

By reducing the probability of retransmission, the effective time each terminal spends in the origination mode also reduces, which indirectly resulted in a low input traffic load. This would suggest that mobile channels might as well be managed by directly controlling the input traffic, for instance by limiting the number of terminals that are allowed to be signed on simultaneously.

Influence of near-far effect

Packet transmissions considered in many theoretical studies are assumed to be uniformly distributed over the coverage area. In this event, the probability of correct reception of one out of n colliding packets has some non-zero limit for large n. As an more realistic alternative, the log-normal spatial distribution can be considered, which assumes log-normally distributed mean powers. This allows more realistic modelling of the packet traffic very close to the receiver. The true uniform distribution is compared with a log-normal distribution. The state probability and average drift are depicted for a receiver threshold of z = 10 (10 dB). The traffic parameters are :

Probability of a new packet arrival in an idle terminal in the next slot P_o = 0.0055,
Probability of retransmission for a busy terminal P_r = 0.08

These and the pessimistic receiver threshold were chosen on purpose such that the two spatial models studied give different assessments of the stability of the network with 100 terminals. While the assumption of a uniform distribution of the offered traffic suggests a stable network with little backlog, the log-normal model predicts bistable performance.

The simulation further takes into account that most retransmissions originate from the boundary of the service area. Initially the software simulation program randomly distributes 100 terminals over the area 0 < r < 1 and estimates the corresponding local-mean powers for every terminal according to plane earth loss ("40 log d"). Shadowing is ignored in this experiment .

All terminal states are modeled as a tri-state variable. In the O state, the program performs a random experiment to simulate generation of a packet with probability P₀. In the R state, permission for retransmission of a previously collided packet is granted with probability P_r. In both cases, the terminal enters the T state where the transmission and (multipath) propagation of a packet is simulated by the random generation of an instantaneous received power, according to an exponential distribution. By accounting for all the received interference packets, the program determines whether any of the colliding packets is strong enough to capture the receiver.

Results indicates that both the uniform and the log-normal spatial distributions lead to optimistic estimates of the network performance, compared to the simulations.

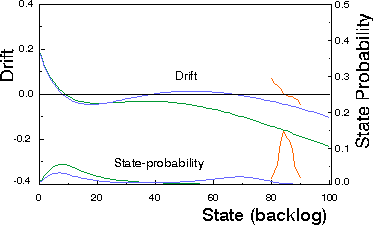
Figure: Expected drift and state probability for a slotted ALOHA network with 100 users and a receiver threshold of z = 10, according to a uniform distribution, a comparable log-normal spatial distribution and a simulation. Probability of a new packet generation P₀ = 0.0055. Probability of retransmission P_r = 0.08.

Because of capture probabilities decreasing with distance, the average time a terminal is in the retransmission mode increases with distance. Since P₀ < P_r , the traffic offered per unit of area increases with distance. This has a disadvantageous influence on the network performance: colliding signals are more often received from far away and hence more with nearly equal (low) powers. Consequently, the probability that the power of one of these signals sufficiently exceeds the joint interference is relatively low.

JPL's Wireless Communication Reference Website

Chapter: Data Networks Section: Random Access, ALOHA