JPL's Wireless Communication Reference Website

Chapter: Analog and Digital Transmission Section: Spread Spectrum , Hybrid DS/FH WISSCE system, BER estimates

Degradation of the data detection SNR

Contributed by Jack Glas, Lucent.

This page covers the performance of an hybrid frequency hopping / direct sequence spread spectrum radio network, in particular the according to the WISSCE system concept. The results of this page are used to calculate the local-mean and instantaneous BER

A number of system properties cause a reduction of the SNR level at the input of the analog to digital conversion. Both non-ideal despreading and multi-access interference degrade the pre-detection SNR value.

Influences of non-ideal despreading

In reality the despreading operation will not be perfect for two reasons: there will always be a misalignment in time between the received signal and the local DS spreading code-generator, secondly there is also an input filter present which affects the received signal.

Timing-misalignment is due to the residual error after code-synchronization. In steady-state operation this error will be small. During code-acquisition however the chip-misalignment can be typically up to a quarter of a chip-period. The autocorrelation-value for small code-misalignments can be written as:

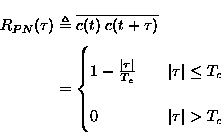$\begin{displaymath} \begin{split} R_{PN}(\tau) &\triangleq \overline{ c(t) \; ... ...\left \vert \tau \right \vert \gt T_c \end{cases} \end{split} \end{displaymath}$

where $\tau$ is the misalignment (timing-error) and T_c is equal to a chip-period. A power correction factor to account for this timing-error is:

$\begin{displaymath} L_t(\tau) = \left ( R_{PN}(\tau) \right ) ^2 \;. \end{displaymath}$

During acquisition this loss may reach 3 dB.
Filtering effects: the input-filter not only removes the signals in adjacent channel, but also suppresses the side-lobs of the intended signal. The power reduction factor can be calculated by the formula:

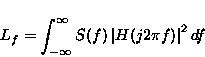$\begin{displaymath} L_f = \int _{-\infty} ^{\infty} S(f) \left \vert H(j 2 \pi f) \right \vert ^2 df \end{displaymath}$

where S(f) is the power spectral density of the input-signal and $H(j 2 \pi f)$ the transfer function of the input filter. A practical situation is illustrated in figure 1, where a second order butterworth filter is used with a bandwidth equal to the chip-rate. The power-loss in this example is 0.5 dB.

**Figure 1:** Effects of input-filtering illustrated
$\begin{figure} \centerline{ \epsfig {figure=\figdir/finfl.eps,width=12cm} }\end{figure}$

This effect results in a trade-off: a narrow filter smooths the autocorrelation curve, but also reduces the output noise power.

Influences of Multi-Access Interference

Multi-access is both the essence and the limitation of CDMA systems. The limit on the maximal number of users results from the amount of interference present in the channel and the desired BER.

Multi-access (MA) interference is present when more than one transmitter is active at the same time. A common way to incorporate multi-access interference in the BER analysis is by modelling this interference as a Gaussian noise component [Pur77,WM92,Ger85]. This approach however assumes that there are numerous interferers which are all received with equal power.

As WISSCE applies a non-cellular transmission concept, the received signal from all users cannot be kept constant by means of power control. To create a handle on this problem, two groups of interferers are distinguished:

1.: A group of interferers relatively far from the receiver (far-interference). The interference caused by this group in total will be translated to a Gaussian noise component following the usual approach. Adding a Gaussian noise component results in a reduction of the input-SNR.
2.: A small group of interferers close to the receiver responsible for the near-interference. This interference cannot be modelled as a Gaussian noise component. Too many of these interferers can block communication links.

There is no clear separation between the two categories. A rule of thumb can be that as long as the signal-power from a user after despreading exceeds the signal-power from the intended user, that user belongs to the category of near-users.

Far interference

This kind of interference is caused by a fairly large group of transmitters relatively far from the reference transmitter. The analysis of this interference is based on concepts from [Ger85,Ger86,Pur77,PS77] adapted for a DS/FH system. If the number of interferers is large, the pseudo-random noise sequences can be assumed to be random. This assumption allows us to derive the variance of the sum of all the far-interference [Roe77]. This variance is equal to the far-interference power and therefore gives the SNR degradation due to far MA-interference. This is illustrated by the following equation for the total detected in energy of a symbol at time n:

$\begin{displaymath} Z(n) = B_{input} T_s N_0/2 + E_s + S~ T_s \text{Var} \left [\sum _{k \neq i} I_{k,i}(n) \right ] \;.\end{displaymath}$

S is the power of the received desired signal and T_s represents the time duration of a symbol period. The first term (B_inputN₀/2) at the right hand side represents noise energy that passes the predetection filter during a symbol time. N₀ is the single sided noise spectral power density [Pro89, p.156]. The second term is the desired energy term (energy per symbol):

$\begin{displaymath} E_s = S~ T_s \;.\end{displaymath}$

I_k,i(n) denotes the amplitude ratio between multi-access interference (user k) and the user signal (user i) during the n^th symbol. The variance of this term is multiplied with the energy per symbol to obtain the interference energy per symbol.

$\begin{displaymath} I_{k,i}(n) = T_s^{-1} \left [ \delta \left (f\;_i^{n}, f\;_... ...{n}, f\;_k^{n+1} \right ) ~ \widehat{R}_{i,k}(\tau_k) \right ]\end{displaymath}$

where the Kronecker function $\delta$ $(\cdot,\cdot)$ is defined by $\delta$ (u,v) = 1, if u = v and $\delta$ (u,v) = 0 otherwise. f_iⁿ is the frequency hopping code for user i during symbol period n. $\tau$ _k is the relative time-delay between the received signals from the intended user and the interfering user k. $R_{k,i}(\tau)$ and $\widehat{R}_{k,i}(\tau)$ are partial cross-correlation terms [SP80].

As a result the first term corresponds to a hit of the users k and i during the earlier part of symbol period n, while the second term corresponds to a hit during the later part of this symbol period. It is also leads to the conclusion that the partial cross-correlation functions $R_{k,i}(\tau)$ and $\widehat{R}_{k,i}(\tau)$ have only influence if a hit occurs.

It is clear that the MA-interference could be divided into two partial interference terms (as illustrated in figure 2). In this figure ``code 1'' of the reference user and ``code k'' of an interfering user are partially overlapping. One term is responsible for the interference in the first part of symbol period and the other term for the second part.

**Figure 2:** Partial interference in DS/FH spreading scheme
$\begin{figure} \centerline{ \epsfig {figure=\figdir/FH-overlap.eps,width=10cm} }\end{figure}$

From the figure it is also clear that in a hybrid DS/FH system, there is at most 1 (partial) hit per symbol-period. This gives:

$\begin{displaymath} \delta \left (f\;_i^{n}, f\;_k^n \right ) \cdot \delta \left... ...criptscriptstyle \vert$}}\vphantom{}\crcr \hbox{\rm\sf N} }}\;.\end{displaymath}$

Taking this into account, formula for the MA-interference can be written as:

$\begin{displaymath} I_{k,i} = \left [~ \delta \left (f\;_i^{n}, f\;_k^n \right ... ...k^{n+1} \right ) \right ] ~\cdot\; T_s^{-1}\; R'_{k,i}(\tau_k)\end{displaymath}$

in which R'_k,i $(\tau)$ is defined as:

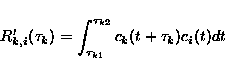$\begin{displaymath} R'_{k,i}(\tau_k) = \int_{\tau_{k1}}^{\tau_{k2}} c_{k}(t+\tau_k) c_i(t) dt \end{displaymath}$

c_k expresses the k^th chip of a pn-code, while $\tau$ _k1 and $\tau$ _k2 are related to $\tau$ _k in the following way:

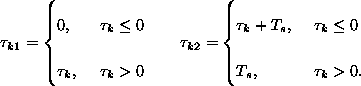
$\begin{gather*} \tau_{k1} = \begin{cases} 0, ~~~ & \tau_k \leq 0 \ \tau_k, & ... ...u_k + T_s, ~& \tau_k \leq 0 \ T_s , & \tau_k \gt 0. \end{cases} \end{gather*}$

This equation for R'_k,i $(\tau)$ is illustrated in figure 3. In this figure the sequences i and k overlap for 5 1/3 chip period.

**Figure 3:** ma-interference illustrated
$\begin{figure} \centerline{ \epsfig {figure=\figdir/overlap.eps,width=12cm} }\end{figure}$

An integer l is now defined which is equal to the number of complete overlapping chips ( $-T_s \leq l T_c \leq$ $\tau$ $_k \leq (l+1) T_c \leq T_s$ , $l~ \in {\ooalign{ \smash{\hskip1.9pt\raise0pt\hbox{\rm\sf Z}}\vphantom{}\crcr \hbox{\rm\sf Z} }}$ ). This number is negative if the later part of code i overlaps with code k. In the example of figure 3 l is equal to 5. The integral for R'_k,i $(\tau)$ can be written as:

$\begin{displaymath} \displaystyle R'_{k, i}(\tau_k) = C_{k, i}(l) \cdot \left [... ...ight ] \displaystyle + \; C_{k, i}(l+1) \cdot [\tau_k - l T_c]\end{displaymath}$

where the first term corresponds to the summation of all ``dark'' overlaps in figure 3 and the second term corresponds to sum of all ``light'' overlaps. C_{k, i}(l) is the discrete aperiodic cross correlation function [PS77]:

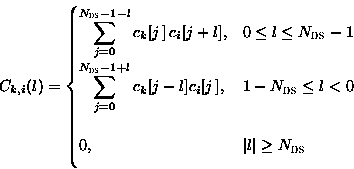$\begin{displaymath} C_{k,i}(l) = \begin{cases} \displaystyle \sum_{j=0}^{N_{... ...splaystyle 0, & \vert l \vert \geq N_{\text{DS}} \end{cases}\end{displaymath}$

where the usage of square-braces expresses the time-discreteness of the pn-codes. If a hit occurs between the intended and interfering user, the variance of the multi-access interference term in the equation for the MA-interference is:

$\begin{displaymath} \text{Var}\left [~I_{k,i}\right ] = {\sigma^2_{k,i}} = \fra... ...T_s^3} \int _{-T_s} ^{T_s} R{'}_{k,i}^2 (\tau_k) \; d\tau_k \;.\end{displaymath}$

The right hand side can be written as (compare with [Roe77,Ger86]):

$\begin{displaymath} \frac{1}{2 \;T_s^3} E \left [ \int_ {-T_s} ^{T_s} R{'}_{k,i... ...= \frac{1}{6\, N_{\text{DS}}} \; E \left [ \rho_{k,i} \right ]\end{displaymath}$

in which:

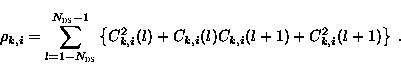$\begin{displaymath} \rho_{k,i} = \displaystyle \sum_{l = 1-N_{\text{DS}}}^{N_{\... ...l) + C_{k, i}(l) C_{k, i}(l+1) + C_{k, i}^2(l+1) \right \} \;.\end{displaymath}$

At this point we will make use of the common assumption that the applied pseudo noise sequences (pn-codes) are random [Roe77,Ger85,Ger86,Pur77,PS77]. After calculation follows for random sequences:

$\begin{displaymath} \text{E}\left [ \rho_{k,i}\right ] = 2N_{\text{DS}}^2 - 1 \approx 2N_{\text{DS}}^2 \;.\end{displaymath}$

This yields:

$\begin{displaymath} E \left [\sigma^2_{k,i} \right ] = \frac{1 }{3 \;N_{\text{DS}}} \;.\end{displaymath}$

The power in the multi-access far-interference term:

$\begin{displaymath} I_{FAR} ~=~ E \left [ \; p_{\text{hit}}(k,K_{FAR}) \right ]... ... \frac{p_{\text{hit}}(k,K_{\text{FAR}})}{ 3\; N_{\text{DS}} }\end{displaymath}$

in which E[p_hit(k,K_FAR)] is the mean number of far-interferers that ``hit'' the reference user in the used frequency-hop channel. E_s denotes the energy per symbol: S T_s.

Concerning the MA-interference the conclusion can be drawn that every far-user that hits the reference user during a FH-period contributes maximally 1/3 N_DS times the desired signal power. To enable the analysis the power of all interfering users was assumed to be equal to the desired power so the equation for the total MA-interference above provides a number on the interference for a worst case scenario.

Near interference

Near interference is more problematic in the sense that it can completely block frequency-hopping channels. When too large a number of such near-users are active, communication is not possible. For this reason the number of near-interferers allowed in the system is limited. The hit-probability (P_hit) is determinative for the performance.

The number of near-users that can be allowed is also determined by the kind of error-correction that is applied. During system-specification it was required at least two frequency-hopping channels have no near-interference. The system specification shows that N_FH is equal to 7 which means that it is likely that there are three near-interference free FH-channels.

Concluding:

it is difficult to give a quantitative analysis of the near-user interference. The amount of interference is to a large extent dependent on the momentary situation. The only thing we can say is that if specifications are met, there will be at least three FH-channels without near-interference.
To enable multi-access interference analysis, the interferers were split into two groups: far-interferers and near-interferers. The interference of the first category of users can be translated into a Gaussian Noise term that deteriorates the input-SNR. The average power that every far-interferer contributes is equal to 1/3 N_DS times the energy per symbol. The second category of interferers is more problematic: a worst case scenario is that only three FH-channels without near-interference.

Conclusion

In this section we saw that the SNR at the input of the A/D converter (after FH-despreading but before DS-despreading) is degraded by:

Timing misalignment with a factor of maximally 3 dB.
Filtering effects with a factor to be calculated by the equation for L_f.
Multi-Access Interference by a factor which can be calculated by the equation above . This term depends on the number of far users as well as pn-code and FH-sequence properties.
Near interference completely suppresses the signal in case a ``hit'' occurs.

Chapter: Analog and Digital Transmission Section: Spread Spectrum , Hybrid DS/FH WISSCE system, BER estimates

JPL's Wireless Communication Reference Website � Jack P.F. Glas (Author) and Jean-Paul M.G. Linnartz (Editor), 1993, 1995, 1999