JPL's Wireless Communication Reference Website

Chapter: Analog and Digital Transmission Section: Spread Spectrum , Hybrid DS/FH WISSCE system, BER estimates

Performance analysis in a Multi-Path Channel

Contributed by Jack Glas, Lucent.

The bit error rate performance is an important performance measure of communication systems. We focus on a hybrid frequency hopping / direct sequence system. results on the instantaneous bit error rate (BER) and the pre-detection SNR are used to calculate the local-mean BER. In particular, we address the WISSCE system.

Flat Rician Channel Model

We assume a frequency-nonselective indoor channel with a Rician distribution of the signal amplitude (Rician fading channel). As we explain in a separate page, for the most short-range indoor systems (including WISSCE) this appeared a reasonable assumption.

Similar to the received power, the signal-to-noise ratio $\gamma$ also has a non-central chi-square distribution: 

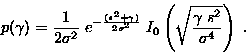
 \begin{displaymath} p(\gamma) = \frac{1}{2 \sigma^2}\; e^{ - \frac{(s^2 + \gam... ...; I_0 \left ( \sqrt{\frac{\gamma\; s^2}{\sigma^4}}\right ) \;.\end{displaymath}

Here s2 is the variance of mean-power of the scattered multipath components and s is the amplitude of dominant line-of-sight component. The Rice factor K is the ratio of LOS-signal power to the random-path signal power. The relation can be expressed as:

s2/2 = $\overline{\gamma}$ K/(K+1) and s2 = $\overline{\gamma}$/(K+1)

Hence, 

            (1+K)e-K         (1+K)                     g
    fg (g) = --------  exp(- ---- g ) I0 (sqrt(4K(1+K) ----) )
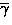
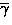
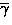
               $\overline{\gamma}$              $\overline{\gamma}$                       $\overline{\gamma}$

$\overline{\gamma}$ is the expectation of $\gamma$ and K is the Rice-factor.

Local-mean BER

The local-mean BER in a Rician fading channel is obtained by averaging over the above pdf of received signal amplitudes. The BER becomes

 

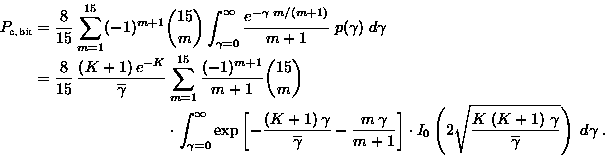
  \begin{displaymath} \begin{split} P_{\text{e, bit}} &= \frac{8}{15} \sum _{m=1... ...line{\gamma}}} \right )\; d\gamma \;. \end{split} \end{split}\end{displaymath}

Performing the integration yields:

 

  \begin{displaymath} P_{\text{e, bit}} = \frac{8}{15} (K+1) \sum _{m=1} ^{15} ... ...e{\gamma}} {(K+1)\,(1+m) + m\,\overline{\gamma}}} \right ] \;.\end{displaymath}

From this formula it is clear that for K = 0 the performance over a Rayleigh fading channel is obtained (see also [Pro89, p.716]). For $R\rightarrow \infty$ the fading effects disappear (compare with the formula for the Static Channel). This is also shown in figure 5 where lines are plotted for R=0 (Rayleigh), K=6.8dB, K=11dB and K=$\infty$ (no fading). Typical values of this parameter for indoor channels at the appropriate frequency are: 6.8 dB and 11 dB [BMS89,Bul87].

See also the special case of Rayleigh fading.

  

Figure 5: ber in a fading-environment
\begin{figure} \centerline{ \epsfig {figure=\figdir/fading2.eps,width=12cm} }\end{figure}


The conclusion of the fading analysis in this section is threefold:

Matlab Code


JPL's Wireless Communication Reference Website © Jack P.F. Glas (Author) and Jean-Paul M.G. Linnartz (Editor), 1993, 1995, 1999