
Code Sequences for Direct Sequence CDMA
with contributions by Frank Kamperman.
In Direct-Sequence CDMA, the user signal is multiplied by a pseudo-noise code sequence of high bandwidth. This code sequence is also called the chip sequence.
The resulting coded signal is transmitted over the radio channel.
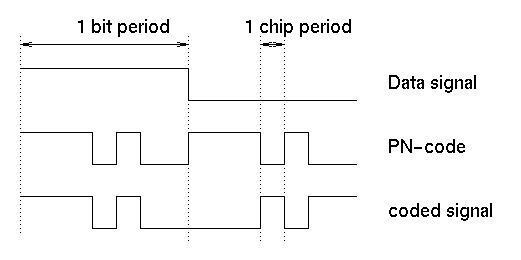
Figure: User signal and code are multiplied to generate the coded transmit signal.
Code Properties
- Autocorrelation
- The (normalized) autocorrelation of the spreading waveform p(t) is defined by
1 inf
Rc(t) = - int p(t) p(t + t) dt
T 0
where p(t) is the transmit waveform of the code, T = Nc Tc is the code period time and t represents a time shift.
- Partial Autocorrelation
- If a bit transition occurs (from +1 to -1 or vice versa), the interference from a delay
CDMA signal consists of two fractions of a bit duration. The Partial Autocorrelation is similar to the above
formula, but integrated only of a portion of the bit duration.
- Crosscorrelation
- Different signals have different spreading codes. The crosscorrelation between two codes i and j is
1 inf
Rc(t) = - int pi(t) pj(t + t) dt
T 0
which equals the autocorrelation if i = j.
Codes Used for CDMA
Popular code sequences used in spread-spectrum transmission are
The names "Pseudo-Noise" (PN) and "maximal-length" are
used in some papers synonymously, while other authors use the name PN sequences to indicate a very broad class of sequences, including for instance ML and Gold sequences.
The user capacity of a synchronous CDMA system, in which the various user signals
exhibit no time offsets when they arrive at the receiver, is limited by the number
of different codes. With a spread factor N and Nu users,
perfectly orthogonal codes can chosen if Nu is less or equal to N.
Welch derived a bound for the maximum normalized cross correlation Rmax
(at zero time offset)
between user codes
(Nu/N) - 1
Rmax2 = ------------
Nu - 1
For Walsh-Hadamard codes N = Nu, so Rmax =0,
and for Gold codes N = Nu - 1, so Rmax=1/N.
Synchronous CDMA is used in the downlink of cellular systems, but multipath reception
can destroy the time alignment of components travelling over different paths.
In asynchronous CDMA, codes arrive in a time-shifted manner, and the crosscorrelation values
typically are much larger.
Asynchronous CDMA occurs in the uplink of cellular systems.
Maximal Length (ML or m) sequences
ML codes
are well understood and have a number of properties which are useful in their application to spread-spectrum systems. For instance
- ML code sequences can simply be generated
by a shift register with feedback.
- ML linear feedback shift-register sequences have very low autocorrelation values. This implies that
- ML sequences can be used in systems that need to operate
in channels with large delay spreads in multipath channels, see e.g. the rake receiver.
- the synchronisation performance is good
See also the page about ML-codes.
Walsh-Hadamard Sequences
If perfectly synchronized with respect to each other, W-H codes are perfectly orthogonal. That is, W-H are optimal codes to avoid interference
among users in the link from base station to terminals.
The simplest matrix of 2 orthogonal Walsh-Hadamard sequences is
1 1
C1 = [ ]
1 -1
The code of user 1 is the first column, i.e., (1, 1), the code of user 2 is the second column, i.e., (1, -1). Clearly (1, 1) is orthogonal to (1, -1).
This matrix can be extended using a recursive technique. For 2n users, the matrix is found from the code
matrix for 2(n - 1) users, according to
C(n-1) C(n-1)
Cn = [ ]
C(n-1) -C(n-1)
Gold Codes
Gold sequences have been proposed by Gold in 1967 and 1968.
These are constructed by EXOR-ing two m-sequences of the same length with each other. Gold sequences have favorable cross-correlation properties.
See also the page about Gold-codes.
Criteria to select a particular code
In synchronous DS-CDMA, the link performance is affected by
- Multi-User interference
- the asynchronous multipath
interference, arising from the delayed signals from
- the other users as well as
- user himself
As the user capacity of the channel is limited by the interference, we would like
to make the partial cross-correlations of
codes small, ideally zero for all time shifts. The values that the partial crosscorrelation
functions take on depend upon the choice of codes. For example, Walsh codes have
the desirable property of perfect orthogonality at zero phase offset, but have
poor autocorrelation properties for other phase offsets. Moreover, Walsh codes
do not spread the signal uniformly over the spectrum. To counteract this, one
scheme has been proposed, e.g. for IS95,
whereby each user's code consists of his unique Walsh code modulated by a ML sequence
common to all users. Good autocorrelation properties are also crucial for timing
recovery and coherent detection.
References
- D.V. Sarwate and M.B. Pursley, "Crosscorrelation properties of pseudorandom and related sequences",
Proceedings of the IEEE, Vol. 68, No. 5, May 1980, pp. 593-619.
- R. Gold, "Optimal binary sequences for spread spectrum multiplexing," IEEE Trans. Information Theory, vol. IT-13, pp. 619-621, 1967.
- M.B Pursley, "Performance evaluation for phase coded spread-spectrum multiple access communication - Part I: System Analysis," IEEE Trans. Comm., COM-25 (August 1977), pp. 795-799.
- E. Geraniotis and B. Ghaffari, "Performance of binary and quaternary direct sequence spread-spectrum multiple-access systems with random signature sequences," IEEE Trans. Comm., COM-39, No.
5, pp. 713-724, May 1991.
- D.V. Sarwate et al, "Partial correlation effects in direct-sequence multiple-access communication systems," IEEE Trans. Comm., COM-32, No. 5, pp. 567-573, May 1984.
- F.D. Garber, M.B. Pursley, "Optimal phases of maximal-length sequences for asynchronous spread - spectrum multiplexing," Electron. Lett., Vol. 16, pp. 756-757, Sept. 1980.






