JPL's Wireless Communication Reference Website

Chapter: Analog and Digital Transmission Section: Spread Spectrum , Hybrid DS/FH WISSCE system, BER estimates

Performance analysis in a Static Channel

contributed by Jack Glas, Lucent.

The bit error rate performance is an important performance measure of communication systems. This page analyzes the receiver behaviour in a hybrid frequency hopping / direct sequence system to find a relation between the bit error rate (BER) and the pre-detection SNR. In particular we address the WISSCE system. This relation needs to be known to formulate requirements for the front-end and the received signal strength.

The BER-analysis is divided into two steps: this section analyzes the situation in which no multipath propagation effects occur is present (additive Gaussian noise channel). The same is done for a multipath environment in the next section. As a reference SNR-level the pre-detection SNR value is used (after FH-despreading at the input of the ADC) where the bandwidth is 1.26 MHz (equal to the chip-rate). The relation between the single-sided noise power ($\sigma$2n), the two-sided noise spectral density (N0/2) and the bandwidth is [Pro89, p.156]:

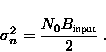\begin{displaymath} \sigma^2_n = \frac{N_0 B_{\text{input}}}{2} \;.\end{displaymath}

The received signal in a single-user, multipath free environment is:

 
 \begin{displaymath} r(t) = \sqrt{S} \; c(t) \exp{ \left [ j \left ( d(t) \Delta_{FSK} + \omega_c \right ) t + \theta \right]} + n(t)\end{displaymath}

where S is the received signal power, d(t) represents the data symbol ({-8, -7, ..., 7, 8}), $\Delta$FSK the MFSK-spacing in radial frequency, c(t) the binary pseudo-random noise sequence, $\omega$c carrier radial frequency, $\theta$ an arbitrary phase and n(t) a noise signal with a two-sided noise spectral density of N0/2.

After DS-despreading the pn-code c(t) is removed from the signal by the local code, for the despread signal x(t) yields:

 
 \begin{displaymath} x(t) = \sqrt{S} \exp{ \left [ j \left ( d(t) \Delta_{FSK} + \omega_c \right ) t + \theta \right]} + n(t) \;.\end{displaymath}

The influence of the despreading operation on the Gaussian noise is small and will therefore be neglected. During MFSK-detection x(t) is, in the 16 MFSK-channels, correlated with the expected signal for the appropriate MFSK-channel. These expected signals can be written as:

\begin{displaymath} v_m(t) = \exp{ \left [ j (m \Delta_{FSK} + \omega_c) t \right ] } \;.\end{displaymath}

The decision variable in the mth channel during the nth symbol-period is via square-law detection found in the following way:

 
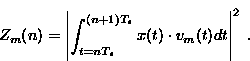 \begin{displaymath} Z_m(n) = \left \vert \int _{t = n T_s} ^{(n+1) T_s} x(t) \cdot v_m(t) dt \right \vert ^2 \;.\end{displaymath}

The decision variable in the MFSK-channel that contains signal (channel i) has a distribution that can be described by a Rician model and a non-central chi-square distribution (sinusoidal signal plus random independent Gaussian inphase and quadrature noise).

Following the analysis in [Pro89, p.295], we will have:

 
 \begin{displaymath} p_{s(i)}(u) = \begin{cases} \displaystyle \frac{1}{2 \si... ... ) & u~ \geq~ 0, \ [1mm] 0 & \text{otherwise.} \end{cases} \end{displaymath}

In which $\gamma$ is the detection (post-despreading) SNR:

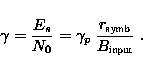\begin{displaymath} \gamma = \frac{E_s}{N_0} = \gamma_p \;\frac{r_{\text{symb}}} {B_{\text{input}}} \;.\end{displaymath}

$\gamma$p is the pre-detection SNR. The factor between the detection and pre-detection SNR is equal to the DS-processing gain. This factor is equal to 18 dB for a DS-sequence length of 63 (Binput/rsymb).

The other channels will contain no signal, the decision-variable will therefore have a central chi-square distribution:

 
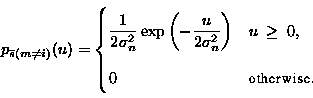 \begin{displaymath} p_{\overline{s}(m \neq i)}(u) = \begin{cases} \displaysty... ...ight ) } & u~ \geq~ 0, \ 0 & \text{otherwise.} \end{cases}\end{displaymath}

A symbol error will occur if the MFSK-channel containing the signal (i) contains less energy than at least one of the other channels. The probability on correct detection can be written as:

 
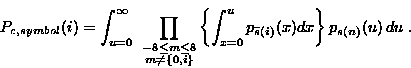 \begin{displaymath} \begin{split} P_{c,symbol}(i) &= \int _{u = 0} ^{\infty} ~... ...line{s}(i)}(x) dx \right \} p_{s(n)}(u) \, du \;. \end{split}\end{displaymath}

Since Zm(n) m$\in$ (-8, -7,..., 8), m $\neq$ {0,i} are statistically independent and identically distributed, the above formula can be written as:


 \begin{align} \begin{split} P_{\text{c, symbol}} &=\int _{u = 0} ^{\infty} \le... ... \binom{15}{m} \frac{e ^{-\gamma \; m/ (m+1)}}{m+1} \;. \end{split}\end{align}

And the bit error rate can be found by (see also [Pro89, p.250]:

 
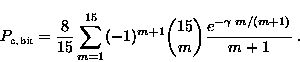 \begin{displaymath} P_{\text{e, bit}} = \frac{8}{15} \sum _{m=1} ^{15} (-1)^{m+1} \binom{15}{m} \frac{e^{-\gamma \;m/(m+1)}}{m+1} \;.\end{displaymath}


  
Figure 4: BER verses input-SNR
\begin{figure} \centerline{ \epsfig {figure=\figdir/berIdeal.eps, width=12cm,height=7.5cm} }\end{figure}

In conclusion we observe that the BER-curve of figure 4 is similar to the usual 16-MFSK BER-curve for these detectors [Pro89, p.297]. The x-axis is however different: this figure has the pre-detection SNR along that axis.

Matlab Code


JPL's Wireless Communication Reference Website © Jack P.F. Glas (Author) and Jean-Paul M.G. Linnartz (Editor), 1993, 1995, 1999