Code Sequences for Frequency Hopping CDMA

Contributed by Jack Glas, Lucent.

In wireless compute networks or wireless LANs with many terminals, (slow) frequency hopping is applied to reduce the problems due to the Near-Far effect. To keep the necessary bandwidth within limits and the frequency synthesizers realizable, the FH-sequence-length (N_FH) is mostly kept small. For instance in the WISSCE concept it is chosen equal to 7. For communication in ISM bands, regulatory agencies often require a minimum spread factor of 10.

For such rather short code-length it is possible to perform a extensive manual search to find possible sequences. As a boundary condition to the sequences we specified that a near-interferer should maximally have 2 hits during a single FH-sequence. A possible code-set existing of 6 sequences is given in table 1.

Table 1: FH-sequences
0 1 2 3 4 5 6

0 2 4 6 1 3 5

0 3 6 2 5 1 4

0 4 1 5 2 6 3

0 5 3 1 6 4 2

0 6 5 4 3 2 1

**Table 1:** FH-sequences
1	2	3	4	5	6
2	4	6	1	3	5
3	6	2	5	1	4
4	1	5	2	6	3
5	3	1	6	4	2
6	5	4	3	2	1

A more general rule can be found in [MT92]. Hyperbolic codes which have the above mentioned property can be formed in the following way: if p is a prime, and there are p frequency-hop channels there exist p-1 codes of length p-1 which have in case of an asynchronous interferer at most 2 hits during a complete FH-sequence. We choose the first alternative because it provides longer sequences.

The hit-probability

The hit-probability is the probability that a number of interfering users are transmitting in the same frequency-hop channel as the reference user. This probability will be referred to as p_h(K), where K is the total number of active users. This probability is dependent on a number of system characteristics like:

The number of frequency-hopping channels available
The number of active users
The kind of frequency-hopping sequences used and their length.

As there are N_FH FH-channels, the chance that two users ``hit'' is 1/N_FH. The FH-sequences are selected on their property to have at most two partial hits which leads to the following hit-probability [Gla92]:

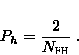$\begin{displaymath} P_{h} = \frac{2}{N_{\text{{FH}\xspace}}} \;.\end{displaymath}$

This formula is only valid if random hopping is applied which is true as a user can start transmitting at any arbitrarily moment.

The chance that 2 users have the same FH-sequence is:

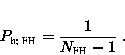$\begin{displaymath} P_{\text{h; {FH}\xspace}} = \frac{1}{N_{\text{{FH}\xspace}} -1} \;.\end{displaymath}$

Two situations can be distinguished:

two users have the same FH-sequence
In this situation, the users will hit always or hit not at all. The first probability is equal to the hit-probability (1).
two users have a different FH-sequence
If two users have a different sequence, they will either have 2 partial hits or a single full hit. So the probability that two users will hit during a ``hop-period'' is: P_hit/N_FH.

We obtain for the complete hit probability:

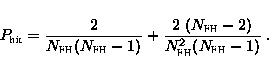$\begin{displaymath} P_{\text{hit}} = \frac{2}{N_{\text{{FH}\xspace}} (N_{\text{... ...}}-2)} {N_{\text{{FH}\xspace}}^2(N_{\text{{FH}\xspace}}-1)} \;.\end{displaymath}$

However, the probability of interest is the chance that a certain number (k) of interfering users are present in the same frequency-hop channel as the intended user. This probability is given by:

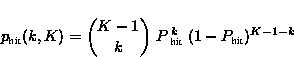$\begin{displaymath} p_{\text{hit}}(k,K) = \binom{K-1}{k}\; P\thinspace^{k}_{\text{hit}} \;(1-P_{\text{hit}})^{K-1-k}\end{displaymath}$

where K is the total number of active users to be considered. In figure 1 the expectation of this probability is shown as a function of K. In this example N_FH is equal to 7. The values from this plot can be used during the calculation of the multi-access interference.

**Figure 1:** $E\left\{p_{\text{hit}}(k,K)\right\}$ as a function of K active users
$\begin{figure} \centerline{ \epsfig {figure=\figdir/hits.eps, width=12cm,height=7.5cm} }\end{figure}$

From the figure above it is clear that even when quite a number of near-users is present, the ``mean'' value of the number of hits is limited to reasonable values.

For the design of the WISSCE system, it was concluded that the receiver should be able to operate under situations where more than 2 FH-channels are blocked. From the figure it appears that even if there are 20 near users, the mean number of hits is about 1.5.

References

Gla92

Jack P.F. Glas.
Definitie en synchronisatie van een ds ffh spread spectrum communicatie systeem voor de korte afstand.
Master's thesis, Delft University of Technology, Faculty of Electrical Engineering, Delft, The Netherlands, June 1992; in dutch.

MT92

Svetislav V. Maric and Edward L. Titlebaum.
A class of frequency hop codes with nearly ideal characteristics for use in multiple-access a spread-spectrum communications and radar and sonar systems.
IEEE Transactions on Communications, COM-40(9):1442-1447, September 1992.

See also: Codes for direct sequence spreading.

JPL's Wireless Communication Reference Website

Chapter: Analog and Digital Transmission Section: Spread Spectrum , Frequency Hopping

Code Sequences for Frequency Hopping CDMA

The hit-probability

References

JPL's Wireless Communication Reference Website © Jack P.F. Glas (Author) and Jean-Paul M.G. Linnartz (Editor), 1999