JPL's Wireless Communication Reference Website

Chapter: Cellular Telephone Networks
Section: Performance Analysis, Telephone Traffic Analysis

Erlang B

Call Blocking in Telephone Systems

In an Erlang-B telephone system, N channels are available. New calls are assigned a channel until all channels are full. Whenever all channels are occupied, a new call is blocked. That is, it is denied a channel. the assumption is that that the calls is lost and that the calling subscriber will not retry again. This in contrast to an Erlang-C system, in which new calls are queued, until they can be served.

Model

The number of active calls is a Markov process, i.e., at any instant t the number of active calls statistically only depends on the number of active calls at t - Dt, with very small D t. New calls arrive according to Poisson process with rate l calls per unit of time. Calls have a (memoryless) exponential duration with mean 1/m. Hence a call terminates with "rate" m and for i calls the rate of termination of one call is i timesm.

 

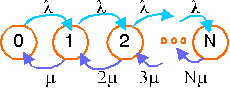Figure: Markov model.
The state (0, 1, ...or N) represents the number of occupied channels in a network with a total of N channels.

 
The probability of being in state i, thus with i channels occupied, can be found from solving the "balance equations" (at equilibrium, the rate of moving into a state should equal the rate of moving out of a state). One finds 

          Ai           1
Pi   =   ---   -----------------
          i!         N      Ai
                     S    ----
                    i=0     i!
where A is the offered traffic expressed in erlang (l/m)
Number of Users

Calls blocked thus far:

%

The random process running here illustrates the number of simultaneous telephone calls in an Erlang B system. There are N = 8 channels available.


Percentage of time spent thus far in state 0 .. 8. Probability of being in state 8 should asymptotically equal the percentage of new calls that is blocked.

Traffic: erlang. Call duration: on average.

It can take a fairly long time before the measured blocking rate resembles the expected value. Click here to stop this animation and remove the animation display. Since the continuous-time process is simulated in discrete time steps, some discrepancies are likely to appear betwen the simulation and the theoretical values, particularly for short average call durations. Thanks to wim Vallenduuk for pointing out that there is a problem here.

PASTA

The "Poisson arrivals see time-averages" (PASTA)-rule says that the probability that a newly arriving call sees a full system equals the time-average probability that the system is in state N. Thus the blocking probability equals PN.

Computer Software

Example and Exercise

A GSM base station uses one carrier of 8 TDMA users. Find the traffic load (in erlang) for which the blocking rate is 1%. Answer


JPL's Wireless Communication Reference Website © 1993, 1995, 2012