|
JPL's Wireless Communication Reference WebsiteChapter: Cellular Telephone Networks |
Contributed by John S. Davis, II, U.C. Berkeley
One main issue in cellular system design reduces to one of economics. Essentially we have a limited resource transmission spectrum, that must be shared by several users. Unlike wired communications which benefits from isolation provided by cables, wireless users within close proximity of one another can cause significant interference to one another. To address this issue, the concept of cellular communications was introduced around in 1968 by researchers at AT&T Bell Labs. The basic concept being that a given geography is divided into polygons called cells.
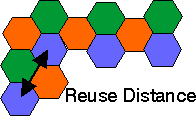
Each cell is allocated a portion of the total frequency spectrum. As users move into a given cell, they are then permitted to utilize the channel allocated to that cell. The virtue of the cellular system is that different cells can use the same channel given that the cells are separated by a minimum distance according to the system propagation characteristics; otherwise, intercellular or cochannel interference occurs. The minimum distance necessary to reduce cochannel interference is called the reuse distance. The reuse distance is defined as the ratio of the distance, D, between cells that can use the same channel without causing interference and the cell radius, R. Note that R is the distance from the center of a cell to the outermost point of the cell in cases when the cells are not circular.
Channel allocation deals with the allocation of channels to cells in a cellular network. Once the channels are allocated, cells may then allow users within the cell to communicate via the available channels. Channels in a wireless communication system typically consist of time slots, frequency bands and/or CDMA pseudo noise sequences, but in an abstract sense, they can represent any generic transmission resource. There are three major categories for assigning these channels to cells (or base-stations). They are
Fixed Channel Allocation (FCA)
systems allocate specific channels to specific cells. This allocation is static and can
not be changed. For efficient operation, FCA systems typically allocate channels in a
manner that maximizes frequency reuse. Thus, in a FCA system, the distance between cells
using the same channel is the minimum reuse distance for that system. The problem with FCA
systems is quite simple and occurs whenever the offered traffic to a network of base
stations is not uniform. Consider a case in which two adjacent cells are allocated N
channels each. There clearly can be situations in which one cell has a need for N+k
channels while the adjacent cell only requires N-m channels (for positive integers k
and m). In such a case, k users in the first cell would be blocked from
making calls while m channels in the second cell would go unused. Clearly in this
situation of non-uniform spatial offered traffic, the available channels are not being
used efficiently. FCA has been implemented on a widespread level to date.
Dynamic Channel Allocation (DCA) attempts to alleviate the problem mentioned for FCA systems when offered traffic is non-uniform. In DCA systems, no set relationship exists between channels and cells. Instead, channels are part of a pool of resources. Whenever a channel is needed by a cell, the channel is allocated under the constraint that frequency reuse requirements can not be violated. There are two problems that typically occur with DCA based systems.
The third category of channel allocation methods includes all systems that are hybrids of fixed and dynamic channel allocation systems. Several methods have been presented that fall within this category and in addition, a great deal of comparison has been made with corresponding simulations and analyses [Cox, Elnoubi, Jiang, Katzela, Yue, Zhang]. We will present several of the more developed hybrid methods below.
Channel Borrowing is one of the most straightforward hybrid allocation schemes. Here, channels are assigned to cells just as in fixed allocation schemes. If a cell needs a channel in excess of the channels previously assigned to it, that cell may borrow a channel from one of its neighboring cells given that a channel is available and use of this channel won't violate frequency reuse requirements. Note that since every channel has a predetermined relationship with a specific cell, channel borrowing (without the extensions mentioned below) is often categorized as a subclass of fixed allocation schemes. The major problem with channel borrowing is that when a cell borrows a channel from a neighboring cell, other nearby cells are prohibited from using the borrowed channel because of co-channel interference. This can lead to increased call blocking over time. To reduce this call blocking penalty, algorithms are necessary to ensure that the channels are borrowed from the most available neighboring cells; i.e., the neighboring cells with the most unassigned channels.
Two extensions of the channel borrowing approach are Borrowing with Channel Ordering (BCO) and Borrowing with Directional Channel Locking (BDCL).
The last nominal channel is most likely to be borrowed by neighboring channels. Once a channel is borrowed, that channel is locked in the co-channel cells within the reuse distance of the cell in question. To be "locked" means that a channel can not be used or borrowed. Zhang and Yum [Zhang] presented the BDCL scheme as an improvement over the BCO method. From a frequency reuse standpoint, in a BCO system, a channel may be borrowed only if it is free in the neighboring cochannel cells. This criteria is often too strict.
|
A Java animation of DBCL is available. This animation page also gives you the opportunity to try your luck as a network operator. |
A natural extension of channel borrowing is to set aside a portion of the channels in a system as dynamic channels with the remaining (nominal) channels being fixed to specified cells. If a cell requires an extra channel, instead of borrowing the channel from a neighboring cell, the channel is borrowed from the common "bank" of dynamic channels. An important consideration in hybrid systems of this type is the ratio of dynamic channels to fixed channels. Analysis by Cox and Reudlink [Cox - 1973] showed that given ten channels per cell, an optimum ratio was 8 fixed channels and 2 dynamic channels. In general, the optimum ratio depends upon the traffic load [Zhang]. In addition to BDCL, a second channel allocation method was presented by Yum and Zhang [Zhang]. Referred to as Locally Optimized Dynamic Assignment Strategy (LODA), this method is best described as a purely dynamic channel allocation procedure as opposed to a hybrid method. In this strategy there are no nominal channels; all channels are dynamic. When a given cell needs to accommodate a call, it chooses from among the bank of available channels according to some cost criteria. The channel with minimum cost is assigned. In a general sense, the cost is a measure of the future blocking probability in the vicinity of the cell given that the candidate channel is assigned. A more detailed description of the cost function will be addressed below.
Similar to the goals of dynamic channel assignment is the process of Dynamic Channel Reassignment (DCR). Whereas a DCA scheme allocates a channel to an initial call or handover, a DCR system switches a cell's channel (that is currently being used) to another channel which is closer to the optimum according to frequency reuse or other cost criteria. Thus, for example, a user communicating with channel n may be switched to channel m during the middle of her/his call if channel m is a more efficient use of the available bandwidth from a frequency reuse point of view. Philosophically, DCR is equivalent to DCA.
A great deal of work is available comparing various realizations of channel allocation schemes [Cox, Elnoubi, Jiang, Katzela, Yue, Zhang]. In comparing performance, typical system metrics include blocking probability of new calls and blocking probability of handover calls. These metrics are written as functions of offered traffic (where the traffic may be written in a variety of forms). It is generally assumed that a blocked new call is preferred over a blocked hand-off call. The idea being that with a blocked hand-off, users are forced to terminate communication in the middle of their session. If this blocking happens at a particularly inopportune time, the results could be disastrous (e.g., business partners cut off in the middle of a vital negotiation). In the case of a blocked new call, at least the business negotiation hasn't started and the involved parties aren't interrupted. Blocking probability is an important metric throughout the field of queueing theory and in the case of M/M/1 queues, the Erlang-B formula is often used for analysis of blocking probability. Because blocked calls can be very disconcerting, systems are typically designed to have blocking probabilities of no more than 1% or 2%. This is consistent with the assumption of small offered traffic loads.
Cox and Reudink were the first researchers to present published comparisons of different channel allocation schemes. Their comparison was based on simulation of an outdoor vehicular wireless communication system [Cox - 1971, Cox - 1972, Jakes]. The simulation divided a region into a grid of square cells. The movement of vehicles had a two dimensional normal distribution with 0 mean and 30 mph standard deviation in each of the two orthogonal directions. Poisson arrivals were assumed for the rate of calls per vehicle and call durations were assume to have a truncated normal distribution (truncated on the left at zero) with a "mean" 90 seconds (true mean of 103.5 seconds).
Cox and Reudink's study considered uniform and non-uniform distributions of spatial traffic. In the uniform case, all cells had approximately the same call arrival rate while in the non-uniform case, some cells had a significantly higher call arrival rate. With both the uniform and non-uniform spatial distributions, fixed channel allocation schemes were optimally matched so that the cells with the greatest numbers of calls had the greatest number of channels to deal with those calls. In both cases of uniform and non-uniform traffic, results showed that for low blocking probabilities, dynamic channel allocation schemes could handle more calls than fixed channel allocation schemes. More specifically, in the case of uniform traffic, the DCA approach outperformed the FCA approach when the blocking probability was lower than 10%. At a blocking probability of 1%, the DCA approach could handle over 10% more calls than the FCA approach. In the case of non-uniform traffic, the DCA approach outperformed FCA for blocking rates up to 60%. At a blocking rate of 1%, DCA could handle almost 70% more calls per cell than FCA. Cox and Reudink performed another comparison involving dynamic channel reassignment in [Cox - 1973]. In this hybrid procedure, the total number of available channels is broken into two groups: fixed and dynamic channels. When a cell requires a channel, it first searches for an available fixed channel that is preassigned to the cell. If none of the fixed channels are available, a dynamic channel is searched for from the common bank of dynamic channels. If this search is in vain, the call is blocked. When users who were assigned fixed channels end their calls, these freed fixed channels are then assigned to users in the same cell who are currently using dynamic channels. This frees the dynamic channel for future use and ensures that a large number of channels being used are the optimally-spaced, fixed channels. Results from Cox and Reudink's study of dynamic channel reassignment showed that channel use was increased by over 60% compared to fixed channel allocation for a blocking rate of 1%. This result corresponds to uniform offered traffic.
Zhang and Yum compared four channel assignment strategies [Zhang and Yum];
With respect to uniform offered traffic, their results showed that BDCL had the lowest blocking probability followed by BCO, LODA and FCA. With non-uniform offered traffic, the relative performance of the four methods was the same with the exception that in this case, LODA performed better than BCO. It makes sense that the ordering for BDCL, BCO and FCA was as found. Indeed, BDCL was specifically designed as an improvement over BCO and BCO was designed as an improvement over FCA [Zhang, Elnoubi]. The fact that the performance of LODA varies under uniform versus non-uniform traffic is rather interesting however. The reason behind this phenomenon is that LODA provides optimal channel allocation only in local regions. Given non-uniform traffic which consists of dense regions in certain local areas, LODA will accommodate these regions of high traffic offering. However, in a global sense, the LODA algorithm will not necessarily provide the optimal allocation. With uniform offered traffic, LODA does not have any regions with peak traffic to optimize; i.e., no local regions within which the benefits of LODA can be realized. Furthermore, with respect to the entire region, the optimization is generally not optimal in a global sense. The result is that with uniform traffic, LODA does not have any advantage to offer over BCO. From the previous discussion we see that one general result of all of the comparisons is that dynamic channel allocation outperforms fixed channel allocation for low blocking rates (below 10% in most cases). Blocking rates above 1% or 2% are generally not tolerated. This is generally an accepted guideline throughout the telecommunications industry and we will adhere to this design constraint as well.
The large array of possible channel allocation systems can become cumbersome. However, all channel allocation methods operate under simple, common principles. Throughout this report we have touched on three points which an efficient channel allocation scheme should address:
As the first requirement suggests, all channel allocation schemes adhere to condition 1. From a frequency reuse standpoint, a fixed channel allocation system distributes frequency (or other transmission) resources to the cells in an optimum manner; i.e., common channels are separated by the minimum frequency reuse distance. Thus, a fixed channel allocation scheme perfectly satisfies condition 3 as well. However, a fixed allocation scheme does not satisfy condition 2.
Philosophically, any dynamic channel allocation scheme will meet the requirements of all of the above three conditions to some degree. At the system architecture level dynamic channel allocation schemes may differ widely, but fundamentally, their only difference is in the degree to which they satisfy condition 3. Different DCA schemes attempt to satisfy condition 3 (in addition to conditions 1 and 2) by approaching the minimum frequency reuse constraint arbitrarily closely, and by doing so in as short a time period as possible. The above three conditions point to the fact that design of dynamic channel allocation schemes falls within the general class of optimization problems. Furthermore, since we can always assume that the available number of base stations is finite and the transmission resources will always be countable (due to FCC requirements if nothing else) then our problem can be reduced to the subclass of combinatorial optimization problems. As with all combinatorial optimization problems, there will exist a solution space and a cost function [Aarts & Korst]. A typical element of the solution space could be a particular layout of frequency channels among the base-stations. The cost function can be loosely characterized as the difference between the frequency reuse of an arbitrary solution and the frequency reuse of the optimized solution. The error associated with a non-optimized cost is realized as a future increased blocking probability or an otherwise unwarranted lack of channel availability. It is typically assumed that the solution to the wireless dynamic channel allocation problem is NP-complete [Yue, Cox - 1971]. The definition of np-completeness follows from the conjecture made in the late 1960's that there exists a class of combinatorial optimization problems of such inherent complexity that any algorithm, solving each instance of such a problem to optimality, requires a computational effort that grows superpolynomially with the size of the problem. In the case of dynamic channel allocation, the complexity is generally attributed to the required inclusion of cochannel interference in any analysis of dynamic channel allocation schemes [Yue]. The author is aware of one published article to date offering an analytical method (approximate) for calculating the performance of dynamic channel allocation [see Yue]. Recently, several approximation techniques have been proposed as methods for solving condition 3 of the dynamic channel allocation problem. In particular there has been interest in applying simulated annealing techniques [Duque-Anton] and neural network methods [Chan, Kunz, Funabiki] to dynamic channel allocation.
ReferencesTry you luck as a frequency assigner in the Dynamic Channel Allocation game.
