JPL's Wireless Communication Reference Website

Chapter: Analog and Digital Transmission Section: Spread Spectrum , Hybrid DS/FH WISSCE system, BER estimates

Channel Fading Model for WISSCE

Contributed by Jack Glas, Lucent.

This page covers the channel modeling assumptions for the BER analysis for the WISSCE system. The following discussions applies more generally to indoor wireless communication systems, e.g. wireless LANs.

Multipath is the effect that the signal received at the receiver does not come as a single beam of line-of-sight directly from the transmitter. Especially in an indoor environment, the transmitted signal will reflect at several places and will reach the receiver via various paths of different length and consequently with unequal time delays. This leads to Rician fading.

Every reflected path having its own propagation delay ($\tau$n) and attenuation factor ($\epsilon$n). If s(t) is a single path signal, the received signal can be written as:

 
 \begin{displaymath} r(t) = \sum_n \epsilon_n(t) s \left [t - \tau_n(t) \right ]\end{displaymath}

where both $\epsilon$n and $\tau$n are functions of time, indicating that the channel is time varying. As both $\epsilon$n and the phase (because of $\tau$n) are randomly changing, r(t) can be modelled as a random process. When there are a large number of paths, the central limit theorem can be applied, i.e. r(t) can then be modelled as a complex-valued Gaussian random process.

Two important parameters in characterizing the channel are the RMS delay-spread and the Doppler spread. The RMS delay-spread is the range of values of $\tau$ for which the channel transfer function is unequal to zero, and is referred to as TRMS. Related to TRMS is the coherence bandwidth of the channel. This bandwidth can be interpreted as the bandwidth over which the channel transfer function does not change: thus two sinusoids with a frequency separation larger than ($\Delta$f)c are affected differently by the channel.

Typical values for the RMS time delay-spread in an indoor environment at frequencies round 910 MHz are in the range of 50 ns up to 250 ns [BMS89]. For the 2.4 GHz band values between 10 ns and 40 ns are reported [JP92,HT94,Nik95]. In WISSCE a chip-period takes about 795 ns which is much longer than TRMS as a consequence there is only a single resolvable path.

The coherence time specifies a time-period over which the channel stays the same. The coherence time (($\Delta$t)c) gives an indication of the speed of the variations of the channel. If is inversely proportional with the Doppler spread. Indoor measurements [HP90] show a maximum Doppler spread of 6.1 Hz. Therefore it is safe to assume that the indoor channel will not change within a symbol period.

Influences of the fading channel

If the channel does not change significantly during a symbol-period, the received signal is:

\begin{displaymath} r(t) = \epsilon ~ e^{-j\;\phi} s(t) + n(t)\end{displaymath}

in which $\epsilon$ is a constant attenuation factor and $\phi$ a constant phase-offset. s(t) is the desired signal and n(t) represents an additive Gaussian noise term.

The data-detection algorithm in WISSCE is independent of phase offsets. Consequently the fading influence lays in the attenuation factor. As a result the detection SNR becomes a random variable. Several ways exist to describe the indoor communication channel [Has93]. The most straightforward technique is to model the received signal amplitude as being Rayleigh distributed. The physical justification for this is that the received signal only contains multipath components. In the receiver the amplitude is equal to the square-root of the summation of the squares of the in-phase and quadrature components. As both those components have a Gaussian distribution, the amplitude will be Rayleigh distributed (Rayleigh fading channel). The SNR is proportional to the received power and consequently, the detection-SNR ($\gamma$) will have a central chi-square distribution with 2 degrees of freedom:

 
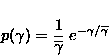 \begin{displaymath} p(\gamma) = \frac{1}{\overline{\gamma}}\; e^{- \gamma / \overline{\gamma}}\end{displaymath}

where $\overline{\gamma}$ is the expectation of $\gamma$. This parameter is equal to the non-faded value of $\gamma$ times the expectation of $\epsilon$2.

In an indoor environment however, often a line of sight (LOS) signal path is present [PMK90]. The resulting amplitude will then be Rician distributed (Rician fading channel) and $\gamma$ will have a non-central chi-square distribution:

 
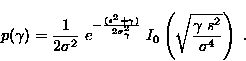 \begin{displaymath} p(\gamma) = \frac{1}{2 \sigma^2}\; e^{ - \frac{(s^2 + \gam... ...; I_0 \left ( \sqrt{\frac{\gamma\; s^2}{\sigma^4}}\right ) \;.\end{displaymath}

Continue with BER calculation for WISCCE over flat Rician fading channel


JPL's Wireless Communication Reference Website © Jack P.F. Glas (Author) and Jean-Paul M.G. Linnartz (Editor), 1993, 1995, 1999