JPL's Wireless Communication Reference Website Chapter: Wireless Channels Section: Multipath Fading

Scatter Function

• Doppler spread (which relate to angles of arrival) and
• path delays.

Figure: the basic idea behind the scatter function is that it plots the expected power per Doppler shift and per excess delay bin. Sometimes, angle of incidence (bearing) is plotted in stead of the Doppler shift.

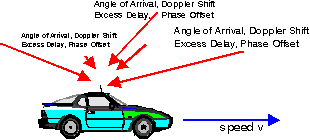Each path can be described by its

• Angle of arrival or Doppler shift
• Excess delay

Thus we can plot the received energy in a two dimensional plane, with Doppler shift on one horizontal axis and delay on the other horizontal axis.

	Environment	Delay Spread	Angle spread	Max. Doppler shift at 1800 MHz
	Macrocellular: Rural flat	0.5 ms	1 degree	200 Hz
	Macrocellular: Urban	5 ms	20 degrees	120 Hz
	Macrocellular: Hilly	20 ms	30 degrees	200 Hz
	Microcellular: Factory, Mall	0.3 ms	120 degrees	10 Hz
	Microcellular: Indoors, Office	0.1 ms	360 degrees	2..6 Hz
	Table Source: A.J. Paulray and C.B. Papadias, "Space-Time Processing for Wireless Communications", Signal Processing Magazine, November 1997, pp. 49-83. Audio commentary: Peter M. Grant, Distinguished IEEE Lecturer 1997, discusses the table parameters (MPEG audio). See also: Full talk, MPEG plug-in on

A Practical Example from Germany

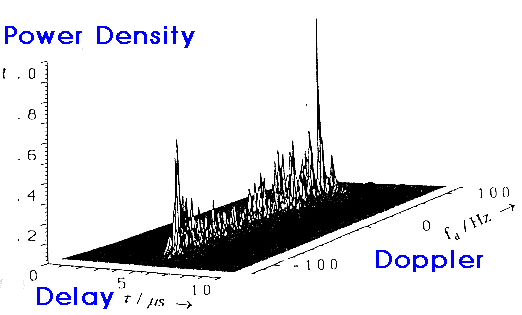
		Figure: measured scatter plot for DCS 1800 MHz system. Doppler spread = 60.3 Hz; Coherence time = 5.9 msec. Delay Spread = 1.2 msec; coherence BW = 1.3 MHz Source: Research group of Prof. Paul Walter Baier, U. of Kaiserslautern, Germany.
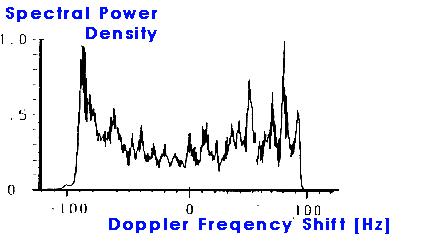
		Figure: Doppler spread corresponding to above scatter plot. Note that the Doppler spread is the projection of the scatter plot on the Doppler frequency axis.
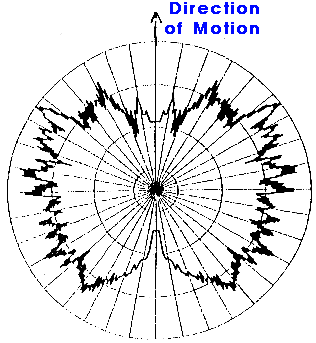
		Figure: Distribution of angle of arrival corresponding to above scatter plot.
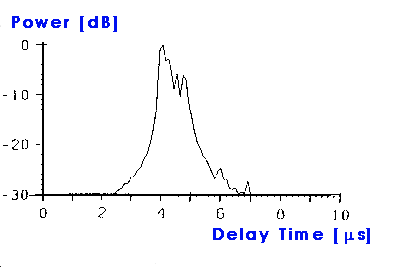
		Figure: Delay spread profile corresponding to above scatter plot. Note that the Doppler spread is the projection of the scatter plot on the time delay axis.

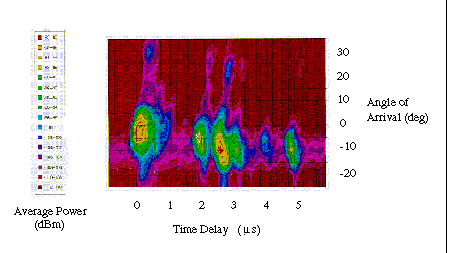
Received power (according to color) versus time of arrival (horizontal axis) and angle of incidence (vertical axis). Source credit: Nortel. Audio commentary: Peter M. Grant, Distinguished IEEE Lecturer 1997. MPEG audio: MP2 ** Power versus delay and angle MP2 Measurement artifacts in delay-angle map See also: Full talk, MPEG plug-in on

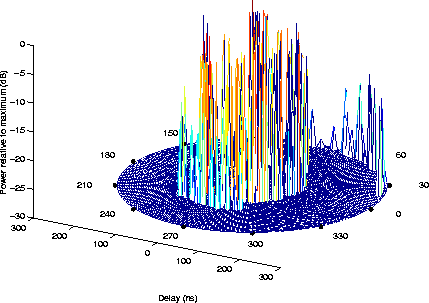
A realization of the local Power Delay-Direction Profile (PDDP). Carrier frequency 5.2 GHz, MT velocity 1 m/s, delay spread TRMS = 50 ns. Such a situation is typical for a small room environment. See the PDDP evaluation by Peter E. Leuthold and Pascal Truffer.

• U-shaped Doppler spectrum, as it occurs with uniformly distributed angles of arrival of reflected waves. The maximum shift is f_m.
• an exponential delay spread with mean T_rms

            Plocal-mean      1               1           t 
  p(f,t) = ------- --------------------  ---- exp(- -----)
            4 p  fm            (f-fc)2     Trms        Trms
                     sqrt( 1 - -------)
                                fm2 

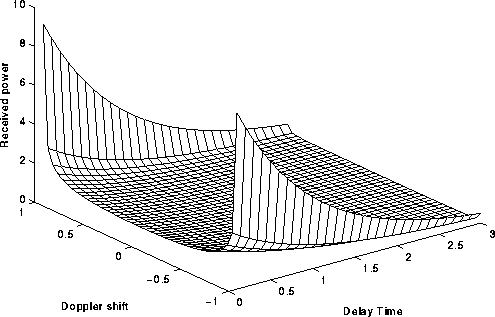
Figure: Scatter function. Received power per unit of frequency shift and per unit of excess time delay.
Frequency shift normalized to the maximum Doppler shift.
Delay time normalized to the delay spread.

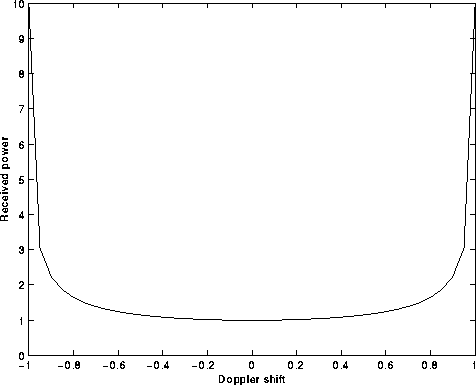
Figure: Scatter function projected to frequency axis. This gives the Doppler spread. Received power per unit of frequency shift.
Frequency shift normalized to the maximum Doppler shift.

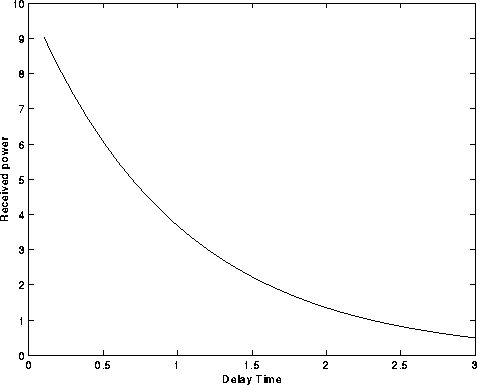
Figure: Scatter function project to delay time axis: This gives the delay profile. Received power per unit of excess time delay.
Delay time normalized to the delay spread.

Channel simulations based on this theoretical model have been contributed by Ralph Haas.

JPL's Wireless Communication Reference Website © Jean-Paul M.G. Linnartz, 1993, 1995.