JPL's Wireless Communication Reference Website

Chapter: Wireless Propagation Channels
Section: Multipath Fading, Rayleigh fading, Coherence Bandwidth

Coherence Bandwidth

Narrowband transmission uses radio signals that see flat fading. The channel may be considered relatively constant over the transmit bandwidth. This criterion is found to be satisfied if the transmission bandwidth does not substantially exceed the 'coherence' bandwidth Bc of the channel. This is the bandwidth over which the channel transfer function remains virtually constant.

One can define 'narrowband' transmission also in the time domain, considering the interarrival times of multipath reflections and the time scale of variations in the signal caused by modulation:
A signal sees a narrowband channel if the bit duration is sufficiently larger than the interarrival time of reflected waves. In such case, the intersymbol interference is small.

Formally the coherence bandwidth is the bandwidth for which the auto co-variance of the signal amplitudes at two extreme frequencies reduces from 1 to 0.5. For a Rayleigh-fading WSSUS channel with an exponential delay profile, one finds 


     Bc = 1/(2 p Trms)
where Trms is the rms delay spread. This results follows from the derivation of correlation of the fading at two different frequencies.

Correlation of Fading

From the delay profile, one can compute the correlation of the fading at different carrier frequencies. See The inverse transform of the delay profile gives the autocorrelation of the complex amplitude of a sinusoidal signal at frequency f1 and f2. 
Delay Profile <- ->    E [H(f1) H*(f2) ]
After some algebraic operations, this can be used to express the auto-correlation and auto-covariance of the amplitude, versus frequency separation f1 - f2.


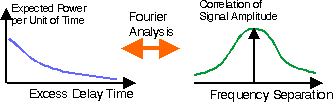
Figure: Auto-Covariance of the received amplitude of two carriers transmitted with certain frequency offset.

The normalized co-variance of the amplitudes R1 and R2 of two carriers, one at f1 and another at f2 is 


      E R1 R2 - E R1 E R2
C =  ----------------------
         s(R1)   s(R2)
That is, we normalized for unity standard deviations sigma of R1 and R2. One finds, for an exponential delay profile 

                      1
C =   --------------------------------
      1 + 4 p2 (f1 - f2)2 Trms2

contents chapter next

JPL's Wireless Communication Reference Website © 1993, 1995, 1999.