JPL's Wireless Communication Reference Website

Chapter: Analog and Digital Transmission
Section: CDMA, Rake Receiver

Analysis of Rake Receiver

The rake receiver is designed to optimally detected a DS-CDMA signal transmitted over a dispersive multipath channel.

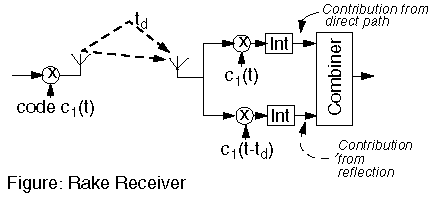Different reflected waves arrive with different delays. A rake receiver can detect these different signals separately. These signals are then combined, using the diversity technique called maximum ratio combining.

Considering antipodal (i.e., BPSK-type) of DS-CDMA, we denote the transmit waveform as m₀ for a digital "0" and -m₀ for a digital "1". The received signal is

r_i(t) = S h_k m_i(t - kT_c) + z(t)

where

the sum S is a summing over all propagation paths k=0, 1, 2, ...,
h_k is the complex amplitude of the k-th propagation path,
T_c is the chip duration,
index i represents the binary message ("0" or "1"), and
z(t) denotes the additive white Gaussian noise.

The power in the k-th resolvable bin is h_k h_k* The local-mean power is

p = E Sh_k h_k*

where E is the expectation operator, applied to find the local-mean value, and * denotes a complex conjugate. We ignore intersymbol interference, that is, we assume that the bit duration T_b is much larger than the rms delay spread T_rms. However, typically T_c < T_rms.

Deriving the Rake Algorithm

In this section we apply the principle of a matched filter to a DS-CDMA signal, received over a Linear Time Invariant (LTI) dispersive channel, with additive white Gaussian noise (AWGN). Using the matched filter theory, we derive the optimum receive algorithm, which is also called a "rake receiver".

An optimal matched filter receiver exploits information of the transmit waveform and the channel characteristics. It correlates the incoming signal r_i(t) with the expected received signal y(t) = S h_k m₀(t - kT_c). The decision variable v becomes

v = Re INT r_i(t) y_i*(t)

where INT is an integration of one bit time. Inserting y_i*(t)

v = Re INT r_i(t) S h_k* m₀*(t - kT_c)

Interchanging integration and summing, we can rewrite this as

v = S Re h_k* INT r_i(t) m₀*(t - kT_c)

Thus, we can implement K correlators, each correlating the incoming signal with the signal waveform m₀*(t - kT_c), time-shifted by kT_c. The outputs of these correlator are weighed by h_k*. Since the signal amplitude is also proportional to h_k, this correspons to maximum ratio combining diversity.

Note that thus far we have not assumed any specific properties of the spreading code.

Bit Error Rate in Fixed, Known Channel

We assume that the receiver perfectly knows and applies estimates of the channel h_k. We insert the received signal r(t) into the decision variable. That allows us to derive the received signal-to-noise ratio and the BER.

v = S_k1 Re h_k1* INT [S_k2 h_k2 m_i(t - k2 T_c) + z(t) ] m₀*(t - k1 T_c)

Here, we simplified the effect of partial correlations. See a more detailed discussion.
Splitting the expression for the devision variable for signal and noise,

v = S_k1 Re h_k1* INT S_k2 h_k2 m_i(t - k2 T_c) ) m₀*(t - k1 T_c)

+ S_k1 Re h_k1* INT z(t) m₀*(t - k1 T_c)

We now use the autocorrelation properties R() of the spreading code, with

R(k1 - k2) = INT m(t - k1 T_c) m(t - k2 T_c) dt

where the integration is over one bit duration, which also equals one period of the code sequence. This gives the following decision variable:

v = S_k1 Re h_k1* S_k2 h_k2 R(k1 - k2)

+ S_k1 Re h_k1* INT z(t) m₀*(t - k1 T_c)

For speading codes with sufficiently good autocorrelation, one typically assumes that R(0) = T_b with T_b the duration of a bit and R(n) = 0 for n not equal to zero. So

v = T_b S_k1 Re h_k1* h_k1

+ S_k1 Re h_k1* INT z(t) m₀*(t - k1 T_c)

So the signal-to-noise ratio in the decision variable is

         T_b² [ S_k1h_k1*h_k1  ]²
    g = ------------------------- = Sg_k 
         N₀T_b   S_k1h_k1*h_k1

The BER is

P = (1/2) erfc[SQRT( S g_k )]

It is important to realize the limitations of this derivation.

The above derivation idealizes the autocorrelation properties of the spreading code.
It considers the presence of one signal in AWGN, but no interference.
If a phase reversal occurs due modulation of the signal, each finger in the rake may see fractions of code sequences from other bins. This leads to increased crosstalk betwen components in the fingers. A more accurate analysis would involve partial autocorrelation functions, to reflect that one sequence changes phase at some point in time.

Bit Error Rate in Rayleigh Channel

According to Rayleigh's model, the channel coefficients h_k are independent complex Gaussian random variables. The power received or the signal-to-noise ratio in the k-th bin of the delay spread is g_k, which is exponentially distributed. Powers in various paths are independent, but usually not identically distributed. The delay profile describes the expected power in each path.

The pdf of S g_k is found considering the Laplace images (or characteristic function) of the pdf of individual received powers. For an exponential signal-to-noise ratio, the image is

U_k(s) = 1/(1+sG_k),

with G_k the local-mean signal-to-noise ratio.

So for all paths combined, the image of the post-combiner signal-to-noise ratio is the product of individual images. Thus,

U(s) = P_k U_k = P_k 1/(1+sG_k),

Inverse transformation yields

f(g) = S C_k /G_k exp(-g_k/G_k)

where

C_k = P_{i, i not equal k} G_k /(G_k - G_i)

We now average the instantaneous BER (for fixed {g_k}) over the pdf of the f(g) . The local-mean BER is

P = (1/2) S_k C_k [ 1- SQRT(G_k / (1+G_k ) ) ]

This expression can be evaluated wity the SPEC, embedded below.

BER SPEC

This Special Purpose Embedded Calculator calculates the BER for a DS-CDMA signal over a dispersive channel with known delay profile.

BER for DS-CDMA

Note 1: Enter a large negative number (e.g. -30 dB) for paths that are not present or for fingers not implemented in the receiver.
Note 2: After you press "calculate", the SPEC re-evaluates all input data. Typically the delay spread is found to be less than initially entered. This is because the above entry fields model an continuous time exponetial delay profile. After sampling at discrete fingers, the delay variability within one bin is no longer modelled. Recalculation of the delay spread from discrete fingers tends to be smaller. Also some power may be lost, if it falls outside the interval covered by the available fingers.
Note 3: Do you see a probability larger than unity? For small outage values, there is an exponent ("e-..") in the outage probability. Some browsers may hide this outside the visible field if they present too many mantissa bits. If you are in doubt, place the cursor in the Outage Probability field and move to the right, beyond the visibile area. Any exponent will scroll into the window.

Pre-programmed default parameters: Exponential delay spread.
RMS Delay spread / Chip duration
Local-mean SNR		dB
Number of fingers in Rake		dB

Resolvable path parameters
Path 1: Local-mean SNR		dB
Path 2: Local-mean SNR		dB
Path 3: Local-mean SNR		dB
Path 4: Local-mean SNR		dB
Path 5: Local-mean SNR		dB
Path 6: Local-mean SNR		dB

Result:
BER for BPSK

JPL's Wireless Communication Reference Website

Chapter: Analog and Digital Transmission Section: CDMA, Rake Receiver

Analysis of Rake Receiver

Deriving the Rake Algorithm

Bit Error Rate in Fixed, Known Channel

Bit Error Rate in Rayleigh Channel

BER SPEC

BER for DS-CDMA

Pre-programmed default parameters:

Resolvable path parameters

Result:

JPL's Wireless Communication Reference Website � 1999.

Chapter: Analog and Digital Transmission
Section: CDMA, Rake Receiver