
|
|
|
Wireless CommunicationChapter:
Analog and
Digital Transmission
|
The rake receiver for direct sequence (DS) spread spectrum can separate energy received over multiple propagation paths with different time delays. Each finger in the rake sees signals with a specific time delay, but it also sees some unwanted residual crosstalk from signals over differently delayed paths. If bit transitions occur in delayed reflection, the crosstalk between two fingers in the rake detector is determined by two partial correlation functions, which exhibit substantially inferior properties than can be achieved for the full (or periodic) autocorrelation function.
If, in a mobile radio channel reflected waves arrive with small relative time delays, self interference occurs. Direct Sequence Spread Spectrum is often claimed to have particular properties that makes it less vulnerable to multipath reception. In particular, the rake receiver architecture allows an optimal combining of energy received over paths with different. It avoids wave cancellation (fades) if delayed paths arrive with phase differences and appropriately weighs signals coming in with different signal-to-noise ratios.The rake receiver consists of multiple correlators, in which the receive signal is multiplied by time-shifted versions of a locally generated code sequence. The intention is to separate signals such that each finger only sees signals coming in over a single (resolvable) path. The spreading code is chosen to have a very small autocorrelation value for any nonzero time offset. This avoids crosstalk between fingers.In practice, the situation is less ideal. It is not the full periodic autocorrelation that determines the crosstalk between signals in different fingers, but rather two partial correlations, with contributions from two consecutive bits or symbols. It has been attempted to find sequences that have satisfactory partial correlation values, but the crosstalk due to partial (non-periodic) correlations remains substantially more difficult to reduce than the effects of periodic correlations.
It can be useful to use of a correlation window in the receiver which is equal to the full period of the spreading code. However, the spreading sequence used by the transmitter is longer than the period used by the correlator for detection. The extension consists of a cyclic prefix for DS-CDMA.
2. A Simple Example
We assume that a logical "1" is represented by a user bit b0 = 1 and a logical "0" is represented by b0 = –1. In Direct Sequence Spread Spectrum, the user data symbols are multiplied with a fast code sequence. For instance the maximum length LSFR code {1,1,1,-1,1,-1,-1} has autocorrelation value 7 for zero time-offset and –1 for time-offsets 1, 2, .. or 6.
After transmission over a multipath channel, the received signal consists of multiple delayed copies of the transmit signal.
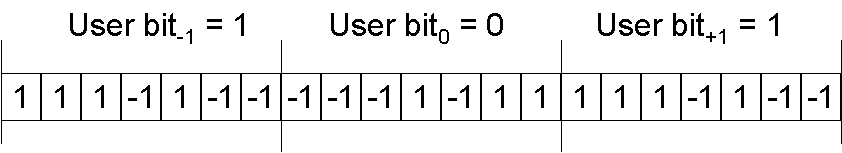
Figure 1: Direct Sequence Spread Spectrum, Three user bits spread by code sequence {1,1,1,-1,1,-1,-1}
The rake receiver for this signal consists of multiple correlators, each synchronized to one of the time offsets of the received signal. In the i-th finger of the rake, the incoming signal is multiplied with the code sequence synchronized to the signal arriving over path i. Let hi be the amplitude of the signal received over path i. If the autocorrelation is good, crosstalk into other fingers is weak, typically M times weaker that the wanted signal, with M the length of the sequence. Because of modulation, the crosstalk is much more severe in a practical situation. The signal Fi seen in the i-th finger consists of three terms, corresponding to contribution from the signal over all three paths. In this case,
Fo= – 7 h0 – h 1 – 3 h 2
F1= – 7 h1 – h 0 + h 2
F2= – 7 h2 – 3 h 0 – h 1
Note that the self-interference from the signal over path 2 is substantially (3 times) larger than would be case for unmodulated carriers, i.e., if b-1 = b0. Hence, ISI occurs.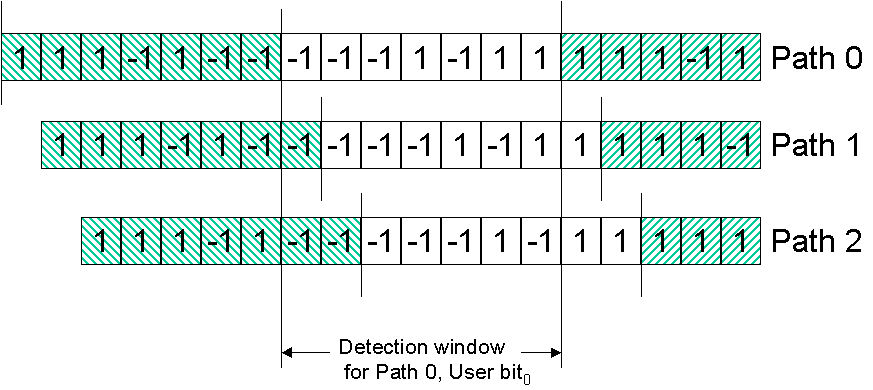
Figure 2: Reception of three delayed waves, over Path 0, 1 and 2. The integration period used in finger 0 of the rake receiver is not well aligned with bit transitions in delayed paths. ISI occurs.
3. Preliminaries and Notation
Without loss of generality we consider the detection of the user bit d0. Due to multipath reception and the associated intersymbol interference, signal components from the previous bit d-1 and the next bit d1 also enter the expression for the decision variable. We use a discrete-time channel impulse response, namely
![]() (1)
(1)
We assume Rayleigh multipath propagation, so the path amplitudes hl are independent complex Gaussian random variables, with variances according to the delay profile. The local-mean power in the i-th bin is
pi = E hihi*
and the total received local-mean power
p = S i pi
The code sequence of user n is denoted as cn(m), where cn(m) = cn(m mod M) with M the length of the sequence. To a large extent we follow previously proposed definitions of correlation functions, but we use a discrete time version. This implies that we do not address the specific issues associated with the pulse shape used for the user bits or of the spread chips. Also we assume that any interarrival time between paths which is not an integer multiple of the chip time, can be written as a linear combinations of integer delays. This is reasonable if the receive system is bandlimited and sampling theory can be applied.
We denote the (periodic or full) cross-correlation function
![]() , (2)
, (2)
the first partial cross-correlation
![]() (3)
(3)
with R<(0) = 0, and the second partial cross-correlation
![]() (4)
(4)
Evidently,
![]() .
.
Exact evaluation of partial correlation function is tedious [3][4]. Moreover the results depend on the particular sequence chosen and on its phase. In the following evaluation, we exploit a few generic properties of binary sequences. Initially we do not assume a specific spreading sequence or class of sequences. We assume that the auto-correlation function Rn,n(k) is known and that the sequences are binary (-1 or 1). An essential part of our analysis is based on the concept that we interpret the (partial or full) correlation function, as a special value of the running sum
![]()
e.g. R<(k) = yk, thus x = k.
We consider yx to behave as a "random walk" which is a priori known to reduce to Rn,n(k) after M steps. Previously this concept was also used in [5]. In the interval m = 0,1, …, M – 1, the terms cn(m)cn(m + k) take on the value "–1" M - times and "+1" M+ times, where
M+ + M - = M
and
M+ - M - = R(k).
Hence,
M + = (M + R(k))/2
and
M - = (M - R(k))/2.
If R<(k) takes on the value l, this requires that k+ terms are positive and k- terms are negative, k+ + k- = k and k+ - k- = l. We must have that k+ £ M+ and k - £ M -. If R(k) < 0 (thus if M+ < M -), the range of values that can be taken on by yx are
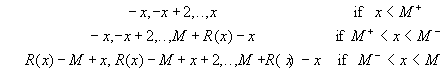
A similar expression can be obtained for R(k) > 0. Figure 4 illustrates the range of yx for R(k) < 0. Note that we plot yx versus the number of terms x using a fixed shift k, where we are particularly interested in x = k and x = M.
We assume that all sequences are equally likely, irrespective of the precise location of the "-1"s and "1"s. We acknowledge that this is may not be true for specific codes, such as m-sequences, which are known to have at most t-1 zero in a row, where t is the length of the LFSR.
The probability that R<(k) takes on the value l is described by (4)
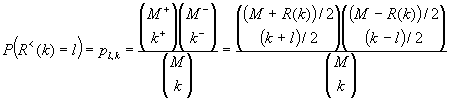
if k + l is even and within the valid range. The probability pl,k equals zero otherwise. Averaged over all codes the second moment of R<(k) equals
![]() (5)
(5)
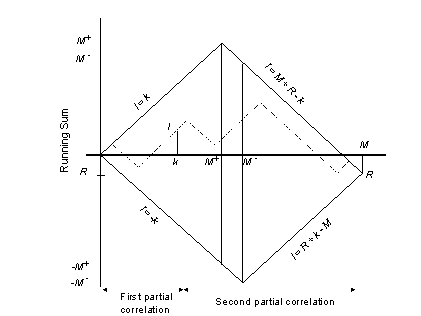
Figure 4: Running sum yx in partial correlation function (R(k) < 0), versus the number of terms considered in the summing. Dotted curve: running sum for specific code, solid lines: worst case. Two sequences shifted over k. R = R(k).
The probability distribution of R>n,n(k) is (6)
![]()
For random sequences with independently chosen zeros and ones, thus without an a priori fixed periodic correlation function, this probability would be
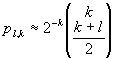 (7)
(7)
for k + l even and –k £ l £ k, and zero otherwise. This expression considers independent values of cn(m) and cn(m + k) for k not equal to 0, thus it ignores the fact that after M steps the random walk returns to zero.
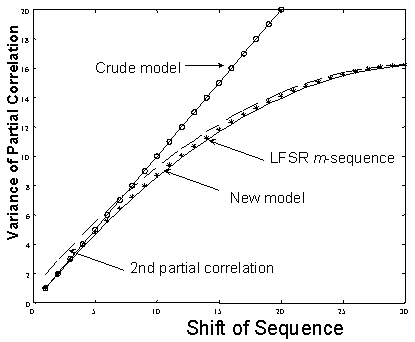
Figure 5: Variance m 2(k) of the first partial
correlation R<(k), (marked with ¾ ) and
approximation for R<(k) (marked with
o).
M = 63.
Experimental results (*) for the set of all (63) shifted LFSR
m-sequences,
generated by polynomial x6 + x + 1. Variance of the
second partial correlation R>(k)
(-
×
-
).
It also serves as an approximation for the usual choice of codes (m,
Gold, or other) provided that these are sufficiently long and studied for small
shifts only (M >> k). Figure 5 plots the variance versus
the shift k. Comparing our model (¾ )
with (*) experiments in Figure 5, we conclude that our model (4) is accurate.
For small k, model (7) is reasonable (see ¾ and o).
4. Performance Evaluation
For a single user channel, the decision variable recovered by the i-th finger (0 £ i £ LR) in the rake is
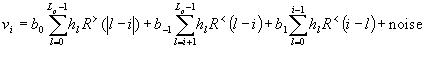 (8)
(8)
Here, the first term represents the "wanted bit" b0, the second and third term describe intersymbol (ISI, or self-) interference from bit b-1 and b+1. See further analysis and comparison with cyclic prefix.