Maximum-Length Sequences

ML code generation

To spread or despread a signal, a spreading function is used which is generated by a spreading-function generator. Here we address the generation and properties of maximal-length (ML) codes. The figure below gives an example of a r-stage shift register for the generation of ML codes.

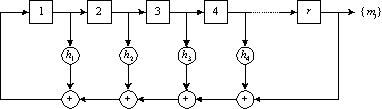
Figure: Shift register for the generation of an ML code

Such shift register implements a primitive polynomial h(x):

h(x) = x^r + h_(r-1) x^(r-1) + .... h₁ x + 1

which is the generator polynomial for a code. In the polynomial h(x), the coefficient h_i takes on the binary value 0 or 1. In practice the coefficients h_i determine the feedback connections in the code generator. For these feedback connections tables exist. The feedback connections, or the corresponding realized polynomial, are represented by the notation

[r, h_(r-1) (r-1), ..., h₁].

where zero-entries are not written explicitly.

Exercise and example

Draw a [3,1] code generator which realizes the polynomial and generates [3,1] codes.

Answer

^TM

sequence generator

ML code properties

The code generator outputs a binary-valued sequence {m_j}. This sequence repeats itself every N_c elements. These elements are called chips. One period of the sequence, thus N_c chips, is called the pseudo noise or spreading code. In DS-CDMA practice, the sequence {m_j} is transmitted mostly as a bipolar waveform p(t), called the spreading waveform. An example is given below.

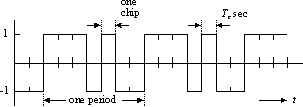
Figure: Waveform p(t) associated with the [3,1] code. (without modulation by a user signal)

ML codes are, by definition, the largest codes that can be generated by a shift register of a given length. For a r-stage shift register their length is N_c = 2^{r - 1}. Thus the [3, 1] code has length N_c = 7.

An important reason for using ML codes is that they have very desirable autocorrelation properties suitable for spread-spectrum systems.

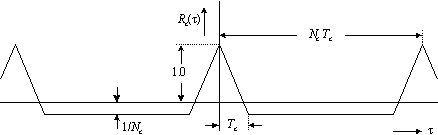
Figure: Auto-correlation for an ML code with chip duration T_c and period N T_c

From the autocorrelation function for ML codes, it follows that this code is indeed suitable as spreading code for spread-spectrum systems. For the autocorrelation function has a clear maximum if t = 0, but is small for any other offset. Due to this property

a spread-spectrum receiver can "easily" recognize code synchronization between the received code and the locally generated (identical) code by examining their correlation value, and
a receiver locked to the dominant wave, only sees little interference from delayed waves, which may be present in a multipath channel.

Code Properties

l Number of LFSR elements	m = 2^l-1 Sequence length	Number of ml sequences	Max. cross correlation, Normalized
3	7	2	0.71
4	15	2	0.60
5	31	6	0.35
6	63	6	0.36
7	127	18	0.32
8	255	16	0.37
10	1023	60	0.37
12	4095	144	0.34

JPL's Wireless Communication Reference Website

Chapter: Analog and Digital Transmission Section: CDMA, Direct Sequence CDMA, Codes.

Maximum-Length Sequences

ML code generation

Exercise and example

ML code properties

Code Properties

JPL's Wireless Communication Reference Website © Jean-Paul M.G. Linnartz1995, 1999.

Chapter: Analog and Digital Transmission
Section: CDMA, Direct Sequence CDMA, Codes.