Exercise

Let z = x + jy with x and y i.i.d. Gaussian with zero mean and variance s².

We initially compute the distribution of received power p. From this the PDF of received power and the PDF of the amplitude can be derived.

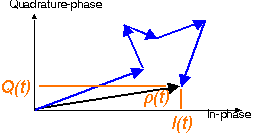
The probability that (x²+y²)/2 < p, with p some power value is

           1                         x²+y²
F (p) =  ----       INT     exp(-   ------)  dxdy
 p       2p s²    x²+y²< 2p             2s²

Using the cartesian to polar transform dxdy = r dr dq, we get

           1       2p       SQRT(2p)        r²
F (p) =  ----     INT   dq   INT  r exp(-   ---) dr
 p       2p s²       0         0             2s²

Thus,

F_p(p) = 1 - exp(- p/s²).

This is the (exponential) distribution of received power p.

The PDF is found by taking the derivative

        1         p
f_p(p) = --- exp(- --)
        s²        s²

The instantaneous power p thus has the above exponential pdf. Conversion between the probability density of amplitude and that of power involves

|f_r(r) dr| = |f_p(p) dp|

and p = r²/2, so dp = rdr. We get:

The pdf of the amplitude is

        r         r²
f_r(r) = --- exp(- --)
        s²        2s²

for r > 0.