
 |
JPL's Wireless Communication Reference WebsiteChapter: Wireless Propagation Channels
|
The wide sense stationary uncorrelated scattering (WSSUS) model is commonly used for multipath fading channels. WSSUS channel assumes that the channel correlation function is invariant over time, and that the scatterers with different path delays are uncorrelated. The WSSUS assumption is realistic to describe the short-term variations of the radio channel.
The fading dispersive channel can be characterized by the complex-valued, time variant, low-pass equivalent channel impulse response h(t,t), where t is the propagation delay and t denotes the absolute time. h(t,t) can be explained as the channel output at time t when the channel input is a unit impulse at time t-t .
For a bandpass signal
s(t)=a(t)cos(2p fct+Q(t)),
in which a(t) is amplitude, fc the carrier and Q(t) the phase of a(t), s(t) can always be expressed as
s(t)=R[u(t)exp(2p fct)]
where u(t)=a(t) cos Q(t)+ ja(t) sin Q(t). Let u(t) go through the channel h(t,t), at the output we get
![]() .
.
It can be written as discrete form,
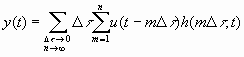 .
.
which enables us to establish a tapped delay-line channel model, as shown in the Figure. This leads to a model where the input is first delayed and then modulated by different tap weights. Delay-line channel model is very useful for us to do channel simulation in time domain.
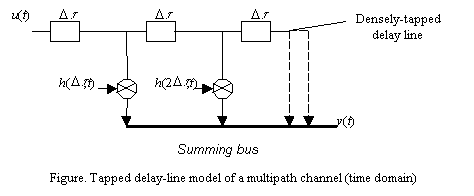
For a WSSUS channel, the autocorrelation function of h(t,t) is
![]()
and f h(t ,D t) is called delay cross-power density. From the above expression, we see that the autocorrelation function does not depend on t but the time difference D t, i.e., it’s Wide-Sense in the time variable. Moreover, the autocorrelation function is zero for D t ¹ 0, i.e., it models Uncorrelated Scattering property in the time-delay variable.
By doing the Fourier transmform of f h(t,D t) on the variable Dt, we obtain the scattering function of the channel
![]()
By integrating the scattering function with respect to t and f respectively, we can obtain the Doppler power spectrum S(f).
![]()
and the delay power spectrum
![]()
Usually, for the channel function h(t, t) we take t = 0 and change t into t, thus the multipath channel can be modeled as a linear filter with a complex-valued impulse response given by
![]()
where hm, i.e., the channel impulse response taps are complex Gaussion distributed and Ts is the sampling resolution of the delay profile. It ensures a densely taped-delay line model when Ts is approximated to zero.