JPL's Wireless Communication Reference Website

Chapter: Wireless Propagation Channels
Section: Multipath Fading, Rayleigh fading, Coherence Bandwidth

Correlation between Complex Amplitude at Two Different Frequencies

In a multipath channel, the relative delay and amplitude of reflected waves are random variables. The correlation between the signal amplitude at two frequencies is denoted as E H(f1) H*(f2).Its derivation is an important step towards the definition of the coherence bandwidth. The delay profile describes the expected energy received in a particular bin of delay times. Here, our analysis diverts from the original derivation, as for instance covered in textbooks by Jakes. By modeling a multipath channel and it delay profile, not as a continuous-time channel but by a time-discrete channel impulse response, sampled at interval Ts, the analysis can be shortened. The generalized time-continuous situation is then covered by taking the limit for Ts decreases to zero.

 

Formulation of the model

Initially we address a discrete-time multipath channel with

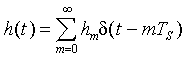
The coefficients hm, i.e., the channel impulse response taps are complex Gaussian random variables. The variance of each tap is determined by the delay profile. For an exponential delay profile with rms delay spread Trms, an appropriate choice is

E hm h*m = [1 - exp{-Ts/Trms}] exp{-m Ts/Trms}

Here the constant [1 - exp{-Ts/Trms}] ensures that the local mean power (found as the sum of E hm h*m over all m) equals unity.

Using the definition of the (continuous time) Fourier Transform, the frequency transfer function for this particular channel is

Correlation

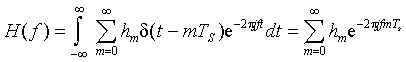
The correlation between the transfer function at frequencies f1 and f2 is

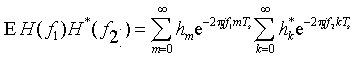
To solve these sums analytically, we substitute q = k - m, so

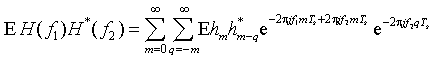
In the summing over q, only the term with q = 0 is non-zero, so


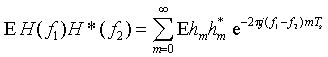
Note that inserting f1 = f2 confirms that the local-mean power E H(f) H*(f) equals the sum of E hm h*m over all m.

Inserting the sampled exponential power delay profile, we arrive at


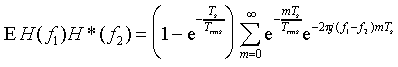
Interpreting the sum as a geometric series gives

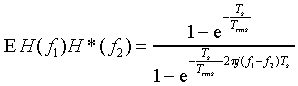
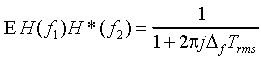
Next we will denote the difference between the two carrier frequencies as Df = f1 - f2. Taking the limit for the sampling resolution Ts of the delay profile reducing to zero,

or


Phase and Quadrature Components

We denote the complex amplitude H(f1) by its in-phase and quadrature components, I1 and Q1, respectively. Similarly, H(f2) = I2 + j Q2 Then,

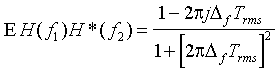
E H(f1) H*(f2) = [I1 + j Q1] [I2 - j Q2] = I1 I2 + Q1 Q2 + j[I2 Q1 -I1 Q2 ].

Further, I1 I2 = Q1 Q2 and I2 Q1 = -I1 Q2. This allows us to split the above expression for E H(f1) H*(f2) into a correlation matrix G for I1, Q1, I2 and Q2.

G= 0.5 [ 10c1c2 ]
01-c2c1
c1 -c210
c2 c101
with

c1 = 1 / [1 +(2p DfTrms)2]

and

c2 = 2p DfTrms / [1 +(2p DfTrms)2]

Note the factor of 0.5, which reflects that half the power is in the I component, and the other half is in the Q component.

Correlation of Real Amplitude

After some mathematical operations and some approximations, one finds that the covariance of amplitudes r1 = SQRT(I12 + Q12) and r2 = SQRT(I22 + Q22) is

E (r1 - E r1) (r2 - E r2) = 1 / [1 +(2p DfTrms)2]

contents chapter next

JPL's Wireless Communication Reference Website © 1999 Jean-Paul Linnartz