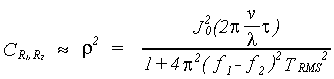JPL's Wireless Communication Reference Website

Chapter: Wireless Propagation Channels
Section: Multipath Fading, Rayleigh fading, Coherence Bandwidth

Coherence Bandwidth

Consider two (random) sinusoidal signals, with sample 1 taken at frequency f1 at time t1 and sample 2 at frequency f2 at time t2. The in-phase and quadrature components I(t) and Q(t of one sample are i.i.d. Gaussian. Also, I1, Q1, I2, Q2 is a jointly Gaussian random vector. The covariance matrix of (I1, Q1, I2, Q2) is

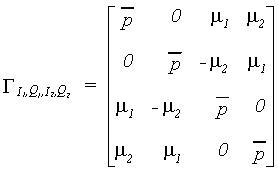
for the most general case, i.e., with non-zero time difference t = t2 - t1, we have


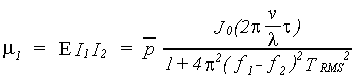
and

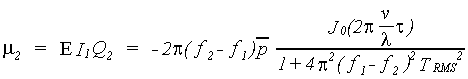
where J0 is the Bessel function of first kind of order 0, and TRMS is the rms delay spread. Note that the Bessel function J0(0) = 1 for zero time differences. We now have to convert I and Q to amplitudes R.

Envelope Correlation (Amplitudes)

The amplitude is found from R12 = I12 + Q12. We convert from (I1, Q1, I2, Q2) to (R1, f1, R2, f2). The associated Jacobian is ½J½ = R1 R2 So the PDF is

f(r1,f1,r2,f2) = r1r2 f(i1=r1cos f1, q1=r1sinf1, i2=r2cosf2, q2=r2sinf2).

Integrating over f1 and f2 gives

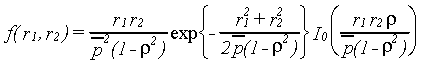
where the Bessel function I0 occurs due to ò exp{cosf} df

The normalized correlation coefficient r is

Envelope Correlation

We now take the expected value E R1R2

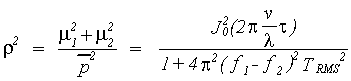
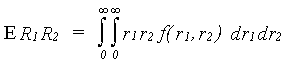
Inserting the PDF (with Bessel function) gives the Hypergeometric integral

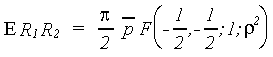
This integral can be expanded as

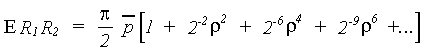
Mostly, only the first two terms are considered

Normalized Envelope Covariance


The normalized covariance takes on values in the interval 0£ C £1

It is defined as

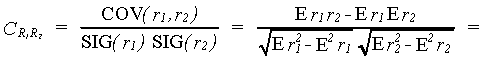
Here we have that

Local-mean value: ER1 = Ö(p/ 2)
Variance: VARR1 = SIG2 R1 = (2 - p / 2)
Correlation: ER1R2 » p /2 [1 + r2 / 4]
Thus, after some algebra,

contents chapter next

JPL's Wireless Communication Reference Website © 1993, 1995.