JPL's Wireless Communication Reference Website Chapter: Wireless Channels Section Rician Channels, Indoor Channels

This K factor is very difficult to measure directly, i.e., by physically isolating the direct wave from the scattered components. However, the K-factor can be estimated from a set of different samples of the channels, for instance at different frequencies.

The method of matching first and second moments was used to determine the Rician K factor. This method sets the sample mean equal to the theoretical mean (both of the received signal amplitude). The following equation shows the theoretical mean of a Rician distributed random variable.

Regarding the second moment, the expectation of E[r²] equals the local mean power, composed of the power in the dominant component, plus the power is scattered components.. Since both the local mean power, , and the sample mean, Er, can be found empirically, this expression can be used to solve for K.

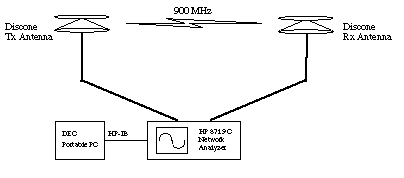
	Figure: Network Analyzer used as Propagation Measurement Setup. Here, a bumper-to-bumper radio communication channel is measures for Autonomous Vehicle Control System (AVCS) applications. The analyzer sends sinusoidal signals at different sample frequencies to the transmit antenna and measures phase and amplitude of the signal coming from the receive antenna. The set-up is controlled by a PC. Data collection and processing is directly done by the PC

Audio

• Audio: Measurement Set-up and Statistical Processing
  The heart of the measurement set-up is a network analyzer. It samples the channel at various frequencies. Channel impulse response are computed from this.
  Using statistical processing on a PC, the r.m.s. delay spread was computed. Also, the Rician K-factor was computed from fluctuations seen in the frequency transfer function.
• Audio: Resolution and Number of Samples
  The network analyzer samples the frequency transfer function in a certain window.
  • The width of the window determines the time resolution of the impulse response.
  • The sampling distance determines aliasing of impulse response.

More on Propagation Measurements

• An interview with Daniel Davarsilvatham on propagation research
• The ECHO 24 channel sounder developed at ETH Zurich
  • full contribution
  • Sounder description

JPL's Wireless Communication Reference Website © John Davis, II and Jean-Paul M.G. Linnartz, 1993, 1995.