JPL's Wireless Communication Reference Website

Chapter: Wireless Channels



Free Space Propagation

 The free space propagation model assumes a transmit antenna and a receive antenna to be located in an otherwise empty environment. Neither absorbing obstacles nor reflecting surfaces are considered. In particular, the influence of the earth surface is assumed to be entirely absent.

For propagation distances d much larger than the antenna size, the far field of the electromagnetic wave dominates all other components. That is, we are allowed to model the radiating antenna as a point source with negligible physical dimensions. In such case, the energy radiated by an omni-directional antenna is spread over the surface of a sphere. This allows us to analyse the effect of distance on the received signal power.

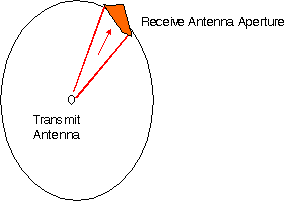
Figure: Transmit antenna modelled as a point source. Transmit power is spread over the surface area of a hypothetical sphere. The receiver antenna has an aperture A, illustrated in orange.

The surface area of a sphere of radius d is 4pd2. The power density w at distance d from a transmitter with power pT and antenna gain Gt is

w = pT Gt/ (4 p d2).

The available power pR at a receive antenna with gain GR is



where A is the effective area or `aperture' of the antenna, with GR = 4p A / l2. The wavelength l is c / fc with c the velocity of light and fc the carrier frequency. The product Gt pT is called the effectively radiated power (ERP) of the transmitter.

20 log d Path Loss Law

As the propagation distance increases, the radiated energy is spread over the surface of a sphere of radius d, so the power received decreases proportional to d-2. Expressed in dB, the received power is


Engineers speak about a "20 log d" path loss law.

Exercise:

Show that the path loss L between two isotropic antennas (GR = 1, Gt = 1) can be expressed as L = - 32.44 - 20 log fc/ 1MHz - 20 log d / 1km, where the loss is found in dB.

Free Space Loss Calculator

Input parameters:
Carrier Frequency: MHz
Distance: meter

Run calculation:
 

 

Result:
Attenuation dB

Field Strength

While cellular telephone operators mostly calculate received power, broadcasters plan of the coverage area of their transmitters using the (CCIR recommended) electric field strength E at the location of the receiver. The conversion formula is

.

Exercise:

Show that for a reference transmitter with ERP of 1 kwatt in free space,



JPL's Wireless Communication Reference Website © 1993, 1995.