
Antenna Gain
 For propagation distances d much larger than the antenna size, the far field of the generated Electromagnetic wave dominates all other components.
The amount of energy radiated in a particular direction (relative to the amount of energy that would be radiated by a theoretical
omni-directional antenna) determines the gain in that direction.
For propagation distances d much larger than the antenna size, the far field of the generated Electromagnetic wave dominates all other components.
The amount of energy radiated in a particular direction (relative to the amount of energy that would be radiated by a theoretical
omni-directional antenna) determines the gain in that direction.
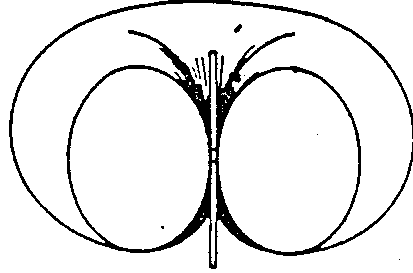
Figure:
Theoretical gain of a dipole antenna
A vertical dipole antenna has constant gain in any horizontal direction, but zero gain
in vertical direction.
The received power at a certain distance can be found from path loss models, such as free space loss.
| | 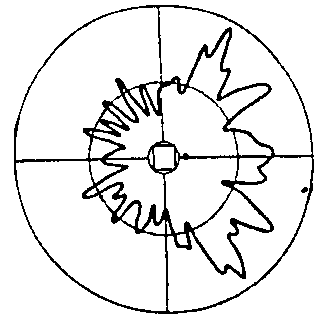 |
Figure: typical gain pattern of an antenna mounted close to a metal tower. Angle-selective fading occurs.
|
|
If multipath scattering occurs near the
antenna, the pattern differs highly from the
theoretical curve, as nulls may occur in certain directions.
This effect is called angle-selective fading.
E and H-fields
|
|

| Antenna theory
describes the magnetic field H and electrical field E
at certain distance from the radiating antenna.
The direction of propagation is the outer product E x H, where E and H lay
on the surface of a sphere centered in the antenna. The direction of propagation
is perpendicular to this sphere.
|

|
|
Conservation of Energy
The total gain of the antenna, integrated over all possible directions
should be unity.
This can be understood from the law of conservation of energy.
The total electric power fed into the antenna equals the total radiated power, provided
that no losses occur.
Omni-directional antenna
One can make an antenna that radiates the same amount of energy in any horizontal direction.
This type of antenna is popular in broadcasting or for cellular base stations
in networks without sectorization. The above vertical dipole is an example of such an antenna.
 However it is theoretically impossible to create an antenna that radiates the same power in all directions, including vertical directions.
The problem is that it is fundamentally impossible to place electric and magnetic field vectors E and H on the surface of a sphere, such that
However it is theoretically impossible to create an antenna that radiates the same power in all directions, including vertical directions.
The problem is that it is fundamentally impossible to place electric and magnetic field vectors E and H on the surface of a sphere, such that
- the E (or H) vector has the same length everywhere,
- remains orthogonal to direction of propagation (i.e., on the sphere surface), and
- the direction of the vector is continuous in every point on the surface.
The non-existance of such field distribution is a fundamental result from topology theory. The same result implies that one can not locate hair on the skin of a cat, such that it can be caressed everywhere.
A discontinuity in the direction of the hair much occur, e.g. at the tip of the tail and on the nose.
 Exercise
Exercise
Explain why the vertical dipole must have a gain larger than unity
in horizontal directions.








 For propagation distances d much larger than the antenna size, the far field of the generated Electromagnetic wave dominates all other components.
The amount of energy radiated in a particular direction (relative to the amount of energy that would be radiated by a theoretical
omni-directional antenna) determines the gain in that direction.
For propagation distances d much larger than the antenna size, the far field of the generated Electromagnetic wave dominates all other components.
The amount of energy radiated in a particular direction (relative to the amount of energy that would be radiated by a theoretical
omni-directional antenna) determines the gain in that direction.


 However it is theoretically impossible to create an antenna that radiates the same power in all directions, including vertical directions.
The problem is that it is fundamentally impossible to place electric and magnetic field vectors E and H on the surface of a sphere, such that
However it is theoretically impossible to create an antenna that radiates the same power in all directions, including vertical directions.
The problem is that it is fundamentally impossible to place electric and magnetic field vectors E and H on the surface of a sphere, such that