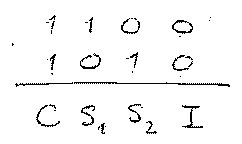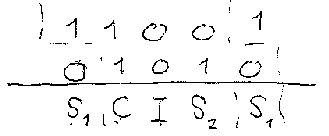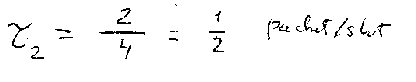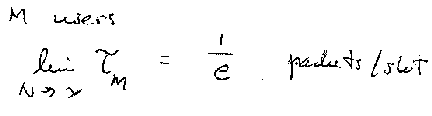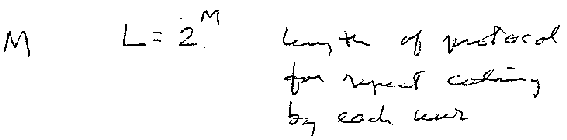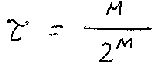Conflict Avoiding Codes: Protocol Sequences
With contributions by James Massey, Boris Tsybakov and Jos Weber
Random Access schemes dynamically assign radio resources to a
large set of users, each with relatively bursty traffic. Conflict-avoiding codes can act as protocol sequences for successful transmission over a collision (random-access) channel without feedback. Such codes guarantee for a certain user the successful transmission of a single packet, despite other users attempting to transmit packets. In contrast to TDMA multiple access, users are unaware of each other's synchronization of attempts.
Formulation of the problem
The time axis is partitioned into slots. The users know the slot boundaries but are otherwise unsynchronized. If in a particular slot none of the users are sending a packet, then the channel output in that slot is the silence symbol. If exactly one user is sending a packet in a particular slot, then the channel output in that slot is this packet value. If two or more users are sending packets in a particular slot, then the channel output in that slot is the collision symbol.
Each user has a protocol sequence, which is a binary sequence of length L that controls his sending of packets within its active period. These sequences should be designed in such a way that for each active user the successful transmission of at least S packets is guaranteed within an active period of L slots. typically S = 1.
The set of the protocol sequences is called a conflict-avoiding code with parameters
M (size of the code, number of potential users),
N (length of the code),
K (maximum number of simultaneously active users), and
S (number of successful packets).
Important results on the collision channel without feedback and conflict-avoiding codes have been presented in [1]-[6].
Applications
ALOHA, CSMA, or polling are methods to collect data from a large set of wireless terminals. These are typically considered
and used for systems collecting road traffic data from cars on a freeway network, power consumption data from meters in house holds,
return signals in an interactive television network, etc.
However all these solutions require a feedback channel.
Protocol sequences can work without a return channel.
|
| 
M3U playlist
| Listen to Jim Massey presenting the concept of protocols sequences.
|
|
|
MP2
SMIL
5'35"
| Protocol sequences describe whether or not time slots are occupied with user data. For instance two users have the sequences 1100 and 1010, respectively.
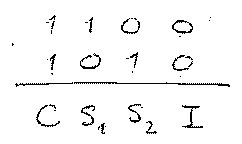
This will lead to one collision, one idle slot and two successful transmissions per frame, no matter what the relative synchronization offset is.
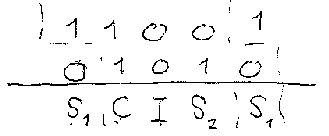
The throughput for N=2 users is
|
|
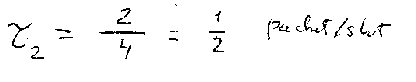
MP2
1'48"
|
For many users, the protocol sequences theoretically have the same throughput as slotted ALOHA.
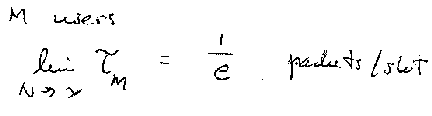
However, the length of the sequence becomes very large.
|
|
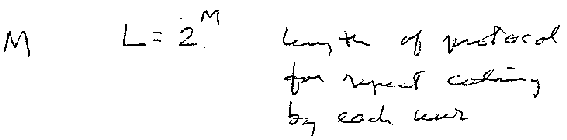
MP2
2'56"
|
|
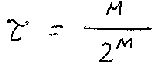
Further Work
As an extension of this concept, Jos Weber and Boris Tsybakov considered codes which can act as the set of protocol sequences for the M possible users of the collision channel without feedback, when it is assumed that at most K users are actively using the channel at any given time.
Their approach is somewhat different: a user session consists of an active period of L time slots, followed by an inactive period of L-1 time slots. The user can begin his next session at any time after the end of his previous session. It is assumed that any active period of any user can have full or partial time intersections with at most K-1 active periods generated by other users. During an active period, the user transmits the packet in each time slot for which the corresponding entry in his protocol sequence equals one and is silent otherwise. During his inactive period, the user is also silent. In order to guarantee at least one successful packet transmission for this user, under the assumption that at most K-1 other sessions are going on during each time slot in the active period of the session, the protocol sequences should satisfy specific properties. The information transmission rate that can be achieved in the described system is R = K/(2L-1).
References
[1] N.Q. A, L. Györfi, and J.L. Massey, "Constructions of Binary Constant-Weight Cyclic Codes and Cyclically Permutable Codes", IEEE Transactions on Information Theory, vol. 38, no. 3, pp. 940-949, May 1992.
[2] L.A. Bassalygo and M.S. Pinsker,"Limited Multiple-Access of a Nonsynchronous Channel", (in Russian), Probl. Inform. Transmission, vol. XIX, no. 4, pp. 92-96, 1983.
[3] L. Györfi and I. Vajda, "Constructions of Protocol Sequences for Multiple Access Collision Channel without Feedback", IEEE Transactions on Information Theory, vol. 39, no. 5, pp. 1762-1765, September 1993.
[4] J.L. Massey and P. Mathys,
"The Collision Channel without Feedback", IEEE Transactions on Information Theory, vol. 31, no. 2, pp. 192-204, March 1985.
[5] P. Mathys,
"A Class of Codes for a T Active Users out of N Multiple-Access Communication System", IEEE Transactions on Information Theory, vol. 36, no. 6, pp. 1206-1219, November 1990.
[6] B.S. Tsybakov and N.B. Likhanov,
"Packet Communication on a Channel without Feedback", Probl. Inform. Transmission, vol. XIX, no. 2, pp. 69-84 (in original Russian version), pp. 147-161 (in English translation), 1983.
[7] E. Sperner,"Ein Satz über Untermengen einer endlichen Menge", (in German), Math. Zeitschrift, vol. 27, pp. 544-548, 1928.
