
 |
JPL's Wireless Communication Reference WebsiteChapter:
Analog and Digital Transmission. Section: Multi-Carrier Modulation
|
A mathematical treatment of OFDM involves
After the qualitative description of the system, it is valuable to discuss the mathematical definition of the modulation system. This allows us to see how the signal is generated and how receiver must operate, and it gives us a tool to understand the effects of imperfections in the transmission channel. As noted above, OFDM transmits a large number of narrowband carriers, closely spaced in the frequency domain. In order to avoid a large number of modulators and filters at the transmitter and complementary filters and demodulators at the receiver, it is desirable to be able to use modern digital signal processing techniques, such as fast Fourier transform (FFT).
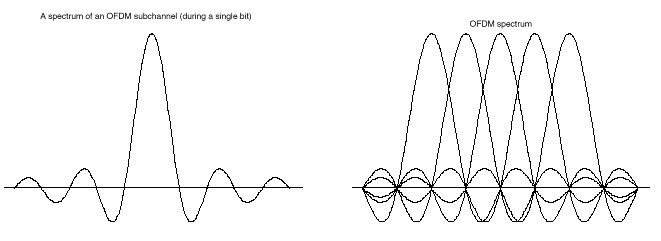
Fig. 4 Examples of
OFDM spectrum (a) a single subchannel, (b) 5 carriers
At the central frequency of each subchannel, there is no crosstalk
from other subchannels.
Mathematically, each carrier can be described as a complex wave:
The real signal is the real part of sc(t). Both Ac(t) and f c(t), the amplitude and phase of the carrier, can vary on a symbol by symbol basis. The values of the parameters are constant over the symbol duration period t .
OFDM consists of many carriers. Thus the complex signals ss(t) (Fig. 4) is represented by:
where
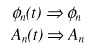
If the signal is sampled using a sampling frequency of 1/T, then the resulting signal is represented by:
At this point, we have restricted the time over which we analyse the signal to N samples. It is convenient to sample over the period of one data symbol. Thus we have a relationship:
If we now simplify eqn. 3, without a loss of generality by letting w 0=0, then the signal becomes:
Now Eq. 4 can be compared with the general form of the inverse Fourier transform:
In eq. 4, the function ![]() is no more than a definition of the signal in the sampled frequency domain,
and s(kT) is the time domain representation. Eqns. 4 and 5 are equivalent
if:
is no more than a definition of the signal in the sampled frequency domain,
and s(kT) is the time domain representation. Eqns. 4 and 5 are equivalent
if:
This is the same condition that was required for orthogonality (see Importance of orthogonality). Thus, one consequence of maintaining orthogonality is that the OFDM signal can be defined by using Fourier transform procedures.
The Fourier transform allows us to relate events in time domain to events in frequency domain. There are several version of the Fourier transform, and the choice of which one to use depends on the particular circumstances of the work.
The conventional transform relates to continuous signals which are not limited to in either time or frequency domains. However, signal processing is made easier if the signals are sampled. Sampling of signals with an infinite spectrum leads to aliasing, and the processing of signals which are not time limited can lead to problems with storage space.
To avoid this, the majority of signal processing uses a version of the discrete Fourier transform (DFT) [van den Enden and Verhoeckx, Oppenheim and Schaffer]. The DFT is a variant on the normal transform in which the signals are sampled in both time and the frequency domains. By definition, the time waveform must repeat continually, and this leads to a frequency spectrum that repeats continually in the frequency domain. [Weinstein and Ebert]
The fast Fourier transform (FFT) is merely a rapid mathematical method for computer applications of DFT. It is the availability of this technique, and the technology that allows it to be implemented on integrated circuits at a reasonable price, that has permitted OFDM to be developed as far as it has. The process of transforming from the time domain representation to the frequency domain representation uses the Fourier transform itself, whereas the reverse process uses the inverse Fourier transform.
The main reason that the OFDM technique has taken a long time to become a prominence has been practical. It has been difficult to generate such a signal, and even harder to receive and demodulate the signal. The hardware solution, which makes use of multiple modulators and demodulators, was somewhat impractical for use in the civil systems.
The ability to define the signal in the frequency domain, in software on VLSI processors, and to generate the signal using the inverse Fourier transform is the key to its current popularity. The use of the reverse process in the receiver is essential if cheap and reliable receivers are to be readily available. Although the original proposals were made a long time ago [Weinstein and Ebert], it has taken some time for technology to catch up.
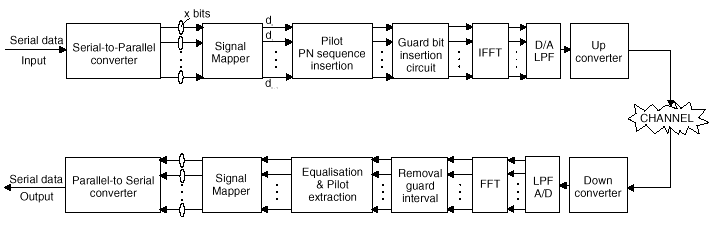
At the transmitter, the signal is defined in the frequency domain. It is a sampled digital signal, and it is defined such that the discrete Fourier spectrum exists only at discrete frequencies. Each OFDM carrier corresponds to one element of this discrete Fourier spectrum. The amplitudes and phases of the carriers depend on the data to be transmitted. The data transitions are synchronised at the carriers, and can be processed together, symbol by symbol (Fig. 5).
The definition of the (N-point) discrete Fourier transform (DFT) is:
and the (N-point) inverse discrete Fourier transform (IDFT):
A natural consequence of this method is that it allows us to generate carriers that are orthogonal. The members of an orthogonal set are linearly independent.
Consider a data sequence (d0, d1, d2, …, dN-1), where each dn is a complex number dn=an+jbn. (an, bn=± 1 for QPSK, an, bn=± 1, ± 3 for 16QAM, … )
where fn=n/(ND T), tk=kD t and D t is an arbitrarily chosen symbol duration of the serial data sequence dn. The real part of the vector D has components
If these components are applied to a low-pass filter at time intervals D t, a signal is obtained that closely approximates the frequency division multiplexed signal
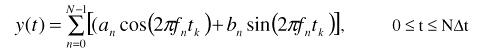 (11)
(11)Fig. 5 illustrates the process of a typical FFT-based OFDM system. The incoming serial data is first converted form serial to parallel and grouped into x bits each to form a complex number. The number x determines the signal constellation of the corresponding subcarrier, such as 16 QAM or 32QAM. The complex numbers are modulated in a baseband fashion by the inverse FFT (IFFT) and converted back to serial data for transmission. A guard interval is inserted between symbols to avoid intersymbol interference (ISI) caused by multipath distortion. The discrete symbols are converted to analog and low-pass filtered for RF upconversion. The receiver performs the inverse process of the transmitter. One-tap equalizer is used to correct channel distortion. The tap-coefficients of the filter are calculated based on the channel information.
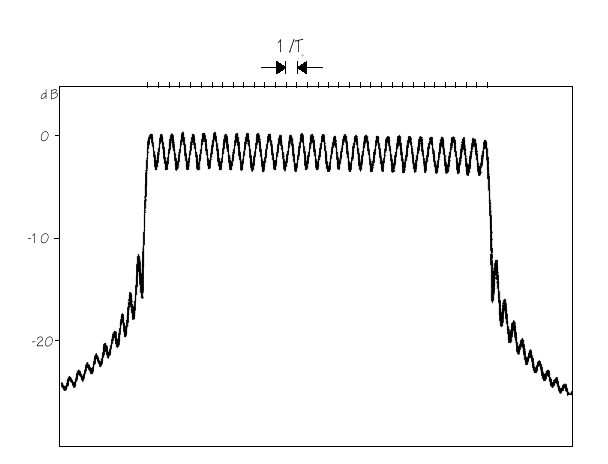
Fig. 6 Example of the power spectral density of the OFDM signal with a guard interval D = TS/4 (number of carriers N=32) [Alard and Lassalle]
Fig 4a shows the spectrum of an OFDM subchannel and Fig. 4b and Fig. 6 present composite OFDM spectrum. By carefully selecting the carrier spacing, the OFDM signal spectrum can be made flat and the orthogonality among the subchannels can be guaranteed.
The orthogonality of subchannels in OFDM can be maintained and individual subchannels can be completely separated by the FFT at the receiver when there are no intersymbol interference (ISI) and intercarrier interference (ICI) introduced by transmission channel distortion. In practice these conditions can not be obtained. Since the spectra of an OFDM signal is not strictly band limited (sinc(f) function), linear distortion such as multipath cause each subchannel to spread energy into the adjacent channels and consequently cause ISI. A simple solution is to increase symbol duration or the number of carriers so that distortion becomes insignificant. However, this method may be difficult to implement in terms of carrier stability, Doppler shift, FFT size and latency.
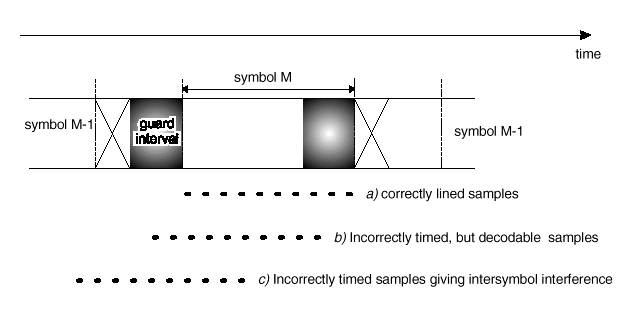
Fig. 7 The effect on the timing tolerance of adding a guard interval. With a guard interval included in the signal, the tolerance on timing the samples is considerably more relaxed.
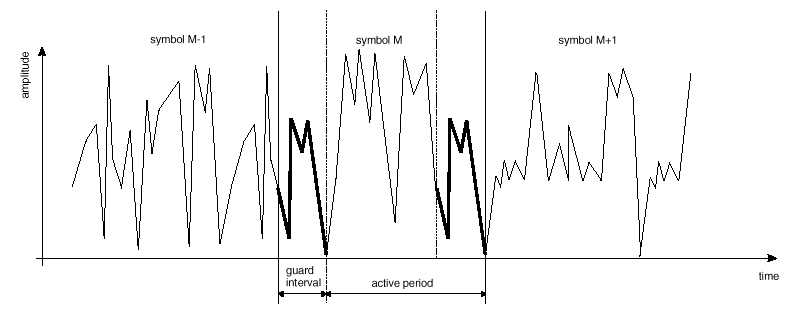
Fig. 8 Example of the guard interval. Each symbol is made up of two parts. The whole signal is contained in the active symbol (shown highlighted for the symbol M) The last part of which (shown in bold) is also repeated at the start of the symbol and is called the guard interval
One way to prevent ISI is to create a cyclically extended guard interval (Fig. 7, 8), where each OFDM symbol is preceded by a periodic extension of the signal itself. The total symbol duration is Ttotal=Tg+T, where Tg is the guard interval and T is the useful symbol duration. When the guard interval is longer than the channel impulse response (Fig. 3), or the multipath delay, the ISI can be eliminated. However, the ICI, or in-band fading, still exists. The ratio of the guard interval to useful symbol duration is application-dependent. Since the insertion of guard interval will reduce data throughput, Tg is usually less than T/4.
The reasons to use a cyclic prefix for the guard interval are: