
JPL's Wireless Communication Reference Website
Chapter: Analog and Digital Transmission
Section: Multi-Carrier Modulation, CDMA,
MC-CDMA

 |
JPL's Wireless Communication Reference WebsiteChapter: Analog and Digital Transmission
|

|
![]()
When MC-CDMA is transtted over a fading channel, the determination of the subcarrier weighing coefficients is to be performed adaptively. Maximum ratio combining (MRC), equal gain combining (EGC) and interference reduction methods can be used. Moreover, the principle of Least-Mean Square Error Estimation can be applied for the detection of Multi-Carrier Code Division Multiple Access (MC-CDMA) signals. It is an optimal filtering method in the sense that it minimizes the mean-square error of the estimated user symbols, with respect to both the noise and the interference.
For an investigation into the theoretical limits we assume that accurate estimates of the complete channel state information (i.e., the fading at the subcarriers) are available and that the coefficients are chosen accordingly. Theoretical results easily can obtained for an MC-CDMA system with a very large number of subcarriers. This model is compared here with simulations for 8 and 64 subcarriers. Simulation results are also presented on the effect of correlated fading (in the frequency domain) at the subcarriers.
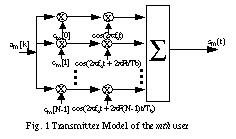 We
denote the vector of the data symbols by A = [
a0[k], a1[k], ..., aN-1[k]
] T, where am[k]
corresponds to the data symbol of the mth user. Define the code matrix
C to be
We
denote the vector of the data symbols by A = [
a0[k], a1[k], ..., aN-1[k]
] T, where am[k]
corresponds to the data symbol of the mth user. Define the code matrix
C to be
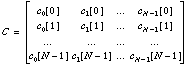
where the mth column vector of C corresponds to the spreading code, Cm = [ cm[0], cm[1], ..., cm[N-1] ] T, of the mth user. Using the vector and matrix notation described above, an equivalent discrete vector representation of the transmitted signal is
S = [ s0[k], s1[k], ..., sN-1[k] ] T = C A
where si[k] represents the signal components of all users at the ith subcarrier for the kth symbol interval. The continuous-time transmitted signal corresponding the kth data symbol of the mth user, am[k], is
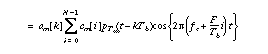
where fc is the carrier frequency and pT(t) is a unit pulse that is non-zero for t in [0,T > and zero otherwise. Note that in a distortionless channel, that data symbol am of the mth user can be recovered using the orthogonality between the codes, as indicated by the following operation
am = (1/N) Cm . S
where the dot denotes the inner product between two vectors. 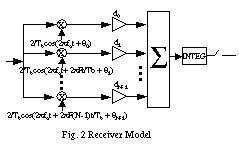
We address downlink transmissions, i.e., from the base station to the user terminals. Similar to common channel assumptions for OFDM systems, the delay spread is considered to be much smaller than the symbol duration. Hence, the effect of the channel at the ith subcarrier may be approximated by a constant amplitude scaling, ri[k], and a constant phase offset, qi[k] over the symbol duration. Using this assumption, the index k will be suppressed throughout the rest of this page.
Applying the received signal to the receiver model, the equivalent discrete representation of the received signal is
Y = [ y0, y1, ..., yN-1 ] T = H C A + Nx
where ym represents the component of the received signal at the ith subcarrier, the channel matrix H is defined to be H = diag[ r0, r1, ..., rN-1 ]. That is,
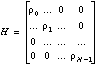 ,
,
and Nx = [ n0, n1, ..., nN-1 ] T is a vector containing the corresponding AWGN terms with ni representing the noise term at the ith subcarrier with power N0/Tb.
The application of the MSE filtering principle to detect signal for user m involves a linear combination of the different subcarrier diversity components to yield the decision variable
n = Dm. Y
where the vector Dm = [ d0, d1, ..., dN-1 ] T represents the optimal weighting coefficients. These coefficients can also be viewed as an amplitude equalization to compensate for the fading at the subcarriers. Arbitrarily choosing m = 0 as the desired signal, the optimal choice of the "equalization" vector D in the mean-squared sense can be determined to be
represents the autocorrelation matrix of the received
vector Y and ![]() represents the cross-correlation vector between the desired symbol, a0,
and the received signal vector, Y. In the formulation of this method,
it is assumed that estimates of the channel amplitudes H, are available
and are consequently treated as deterministic constants.
represents the cross-correlation vector between the desired symbol, a0,
and the received signal vector, Y. In the formulation of this method,
it is assumed that estimates of the channel amplitudes H, are available
and are consequently treated as deterministic constants.
A closed form solution is difficult to obtain except for the case of a full load, i.e., when all N users are active. The corresponding equalization coefficient at the ith subcarrier for a full load is
As expected, the linear combination of the subcarrier components should include the inner product of the desired user's spreading code vector with the received signal vector. For small subcarrier amplitudes r, the equalization coefficient should be small to avoid excessive amplification of the noise. For large r, the correction factor should be proportional to taking the inverse of the channel, 1/r, in order to restore the orthogonality between users.
For sufficiently large values of N, the average bit error rate (BER) for the case of a full load may be approximated using the Central Limit Theorem by
where the signal amplitude per subcarrier is weight wi = di ri, or
![]()
and the interference arrives with amplitude vi
![]() .
.
In obtaining this expression, independent and identically distributed (IID) fading at the subcarriers was assumed.
To study the effect of correlated fading through simulations, an algorithm for generating correlated Rayleigh r.v.s was used.
 Due to the
lengthy computation time for the simulations, results for only spreading factors
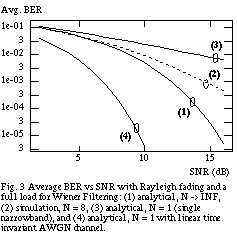
of N = 8 and N = 64 were obtained. Shown in Fig. 3 is a plot of
the average BER versus the signal-to-noise ratio (SNR) in a Rayleigh fading
channel for a full load with N = 8. I.I.D. fading at the subcarriers
is assumed. It is also assumed that all users are received with equal power.
Note that the analytical results for MSE filtering differ significantly from
the simulation results for large SNR. This discrepancy is due to the application
of the Central Limit Theorem to small spreading factors. Shown in Fig. 4 are
the results for N = 64. Examining Fig. 3 and 4, it can be seen that the
approximation is more accurate for large N. Also included in Fig. 3 are
the curves for a single narrowband subcarrier with AWGN, and with and without
fading. Note that the performance of MC-CDMA is better than a single narrowband
transmission due to frequency diversity even with a fully loaded system.
Due to the
lengthy computation time for the simulations, results for only spreading factors
of N = 8 and N = 64 were obtained. Shown in Fig. 3 is a plot of
the average BER versus the signal-to-noise ratio (SNR) in a Rayleigh fading
channel for a full load with N = 8. I.I.D. fading at the subcarriers
is assumed. It is also assumed that all users are received with equal power.
Note that the analytical results for MSE filtering differ significantly from
the simulation results for large SNR. This discrepancy is due to the application
of the Central Limit Theorem to small spreading factors. Shown in Fig. 4 are
the results for N = 64. Examining Fig. 3 and 4, it can be seen that the
approximation is more accurate for large N. Also included in Fig. 3 are
the curves for a single narrowband subcarrier with AWGN, and with and without
fading. Note that the performance of MC-CDMA is better than a single narrowband
transmission due to frequency diversity even with a fully loaded system.
The average BER versus the SNR for correlated fading was also examined for the case of N= 8 (see Fig. 5). The degree of correlation was measured in terms of
![]() .
.
Small a's correspond to highly correlated fading at the subcarriers while large a's correspond to I.I.D. fading. Ideally, the larger the value of a, the higher the degree of frequency diversity. In a DS-CDMA system, the number of resolvable paths L is determined by the ratio between the delay spread Td and the chip duration Tb/N
![]() .
.
Note that for a = 0.125 (L = 2) most of the benefits in performance from frequency diversity have already been achieved.
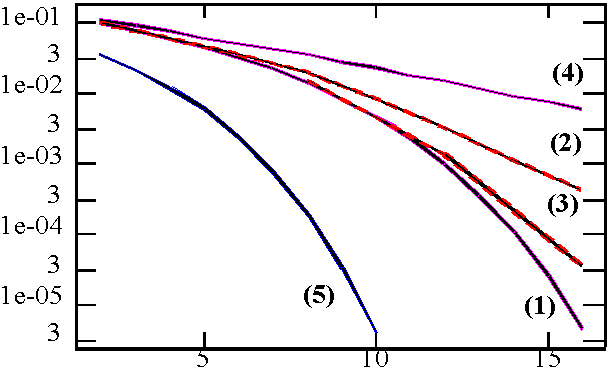
Local-mean average BER versus Signal-to-Noise ratio.
Purple (1): Theorectical curve, single carrier (N = 1)
Blue (2): Theoretical curve, BPSK, no-fading, AWGN
Purple (3): Theorectical curve, infinitely many subcarriers
Red (4): Simulation N = 64
Red (5): Simulation N = 8
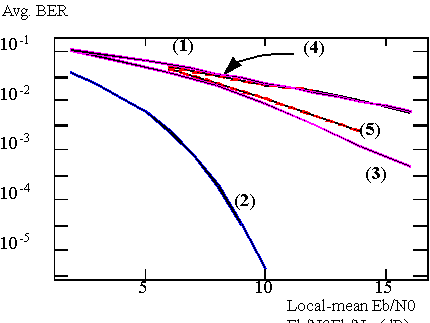
Local-mean average BER versus Signal-to-Noise ratio.
Purple (1): Theorectical curve, single carrier (N = 1)
Blue (2): Theoretical curve, BPSK, no-fading, AWGN
Purple (3): Simulation N = 8, uncorrelated fading
Red (4): Simulation N = 8, correlated fading
Red (5): Simulation N = 8, correlated fading
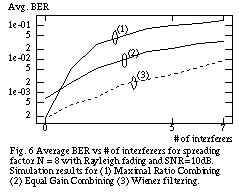
The figure below plots the simulation results for the average BER versus the number of interferers. The SNR was chosen to be 10dB. Because of the time-consuming nature of the simulation, a relatively small spreading factor of N = 8 was used. Besides the curves for MSE filtering, the simulation results of conventional EGC and MRC detection are also included, where
As expected, MSE filtering outperforms EGC and MRC substantially in combating interference.
Even with a full load, MC-CDMA with MSE filtering outperforms single narrowband transmissions in a Rayleigh fading channel. It was also shown that MSE filtering outperforms conventional detection methods substantially. Analytical approximations for many subcarriers appeared reasonably accurate for SNRs up to 12dB and for N = 64 subcarriers. As the number of subcarriers is increased, the accuracy of the analytical results improves.. It was also shown that most of the benefits of frequency diversity can be achieved even in a channel with a significant degree of correlated fading at the subcarriers.
[94-C10] PS PDF PDF2 N. Yee and J.P.M.G. Linnartz, "Wiener filtering for Multi-Carrier CDMA", IEEE / ICCC conference on Personal Indoor Mobile Radio Communications (PIMRC) and Wireless Computer Networks (WCN), The Hague, September 19-23, 1994, Vol. 4, pp. 1344-1347.
PDF J.P.M.G. Linnartz, "Performance Analysis of Synchronous MC-CDMA in mobile Rayleigh channels with both Delay and Doppler spreads", IEEE VT, Vol. 50, No. 6, Nov. 2001, pp 1375-1387.