Rate of Rayleigh Fading

Consider the following sample of a set of reflected waves:

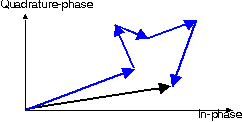
Figure: Phasor diagram of a set of scattered waves (in blue), resulting a Rayleigh-fading envelope (in black)

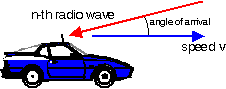
Let the n-th reflected wave with amplitude c_n and phase arrive from an angle relative to the direction of the motion of the antenna.

If the mobile antenna moves a small distance e, the n-th incident wave, arriving from the angle with respect to the instantaneous direction of motion, experiences a phase shift of

 2 pi  e
---------  cos()

Thus all waves experience their own phase rotation. The resulting vector may significantly change in amplitude if individual components undergo different phase shifts.

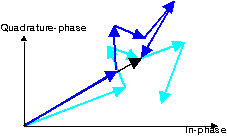
Figure: Phasor diagram of a set of scattered waves after antenna displacement (in blue) and before motion (in light blue), resulting a Rayleigh-fading envelope (in black)

In mobile radio channels with high terminal speeds, such changes occur rapidly. Rayleigh fading then causes the signal amplitude and phase to fluctuate rapidly.

If e is in the order of half a wave length (/2) or more, the phases of all incident waves become mutually uncorrelated, thus also the amplitude of the total received signal becomes uncorrelated with the amplitude at the point of departure.

Doppler Shifts

Each reflected wave experiences its own Doppler shift. If an unmodulated carrier is being transmitted, a spectrum of different components is received.

Autocovariance

The normalised covariance L(e) of the electric field strength for an antenna displacement e is of the form

          2     2 pi  e
L(e)  =  J   ( --------)
          0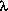

with J_0(.) the zero-order Bessel function of the first kind.
The signal remains almost entirely correlated for a small displacement, say e< /8, but becomes rapidly independent for larger displacements, say for e > /2.

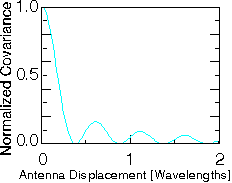
Figure: Auto-covariance L(e) of the electric field strength in a Rayleigh-fading channel versus the normalised antenna displacement e/ (or T f_m) in horizontal direction.

The antenna displacement can also be expressed in the terminal velocity v and the time difference T between the two samples (e = v T). So with f_m the maximum Doppler shift (f_m = v f_c / c).