Doppler spectrum

Doppler shifts

We consider a Rayleigh fading signal. Let the n-th reflected wave with amplitude c_n and phase

arrive from an angle

relative to the direction of the motion of the antenna.

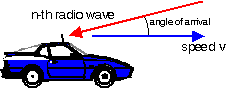
The Doppler shift of this wave is

where v is the speed of the antenna.

The maximum Doppler shift occurs for a wave coming from the opposite direction as the direction the antenna is moving to. It has a shift

            v       
    f_m  = -- f_c
            c

with f_c is the carrier frequency and c the velocity of light.

Such motion of the antenna leads to (time varying) phase shifts of individual reflected waves. It is not so much this minor shift that bothers us in mobile reception, as a receiver can easily compensate for it. Rather, it is the fact that many waves arrive, all with different shifts. Thus, their relative phases change all the time, and so it affects the amplitude of the resulting composite signal. So the Doppler effects determine the rate at which the amplitude of the resulting composite signal changes.

Doppler Power Spectrum

It is often assumed that many waves arrive each with its own random angle of arrival (thus with its own Doppler shift), which is uniformly distributed within [0, 2 pi], independently of other waves. This allows us to compute a probability density function of the frequency of incoming waves. Moreover, we can obtain the Doppler spectrum of the received signal.

This leads to the U-shaped power spectrum for isotropic scattering,

                      1               1
         S(f)  =  --------  -------------------------
                  4 pi f_m                (f-f_c)^2
                             sqrt( 1 -   -----------)
                                            f_m^2

where we assumed a unity local mean power.

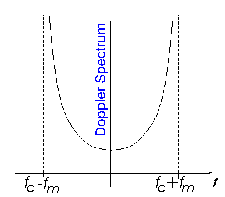
Figure: Power density spectrum of a sine wave suffering from a Doppler spread.

If a sinusoidal signal is transmitted (represented by a spectral line in the frequency domain), after transmission over a fading channel, we will receive a power spectrum that is spread according to the above image. The frequency range where the power spectrum is nonzero defines the Doppler spread.

More details

An animation of fading
Samples of a Rayleigh channel.
Slides for a derivation of the spectrum
Scatter Function

How do systems handle Doppler Spreads?

Analog

Carrier frequency is low enough to avoid problems

GSM

Channel bit rate well above Doppler spread
TDMA during each bit / burst transmission the channel is fairly constant.
Receiver training/updating during each transmission burst
Feedback frequency correction

DECT

Intended for pedestrian use:
- Only small Doppler spreads are to be anticipated
- Bit rate is very large compared to Doppler spread.

IS95 Cellular CDMA

Downlink: Pilot signal for synchronization and channel estimation
Uplink: Continuous tracking of each signal

www.WirelessCommunication.NL

Chapter: Wireless Channels Section: Multipath fading, Rayleigh fading