

|
Wireless CommunicationChapter: Analog and Digital
Transmission
|
Various definitions of BER's are relevant to a system designer: the instantaneous BER B0 of an individual subcarrier with a given amplitude, and the local-mean BER B1, thus averaged over all channels. We compute B0 as the BER for a given b n,n, but otherwise averaged over all channels, i.e., averaged over b m,n (m ¹ n). That is, B0 can be interpreted as the expected value of the BER if only the subcarrier amplitude is known (or estimated) from measurements, but without any knowledge about the instantaneous value of the ICI. A typical OFDM receiver would forward such side information to the error correction decoder.
We consider a quasi-stationary radio link, in which channel variations cause ICI, but the power P0 = b n,nb n,n*/2 for each subcarier is reasonably constant during an OFDM frame. Formally these two assumptions conflict, but for small Doppler shifts they may be reasonably accurate [10-11]. For OFDM, the instantaneous signal-to-noise-plus ICI ratio g equals
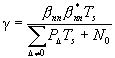 (10)
(10)
We calculate BER's for BPSK, however the usual QAM can be expressed with similar formulas. In a Rayleigh channel, b m,n results from the addition of many independent waves, so it is a complex Gaussian random variable [17]. The contributions to the ICI become Gaussian, so the BER B0 = erfc(Ö g ). Moreover, since b n,n is complex Gaussian, b n,nb n,n* has an exponential distribution with mean P0. Therefor, the SNR g has the probability density fg (g )= g lm -1 exp{-g lm-1 g } with local-mean SNR
g lm = P0 Ts /( N0 + Ts S (D¹ 0) PD ).
After averaging, the local-mean BER for BPSK modulation becomes (see computation for BER for Rayleigh fading)
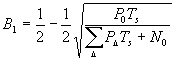 (11)
(11)
In the denominator, the summing is over all integer D within the range of active subcarriers, thus including D = 0.
See also local-mean SER for QAM in Rayleigh fading channel.
For engineering applications with small Doppler spreads, a rule of thumb can be derived by considering only ICI for adjacent subcarriers and by making a first-order approximation for the sinc. For arguments near zero, we take sinc(f fs-1) » 1, so we find that P0 » PT. For D = 1 (and for f << fs), we approximate sinc(1 + f fs-1) » sinc(1) + (1 + f fs-1 - 1) sinc'(1) = f fs-1. Moreover we observe that P1 = P-1. Inserting these, and using eq. 2.272.3 in [20], we find
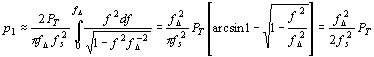 (12)
(12)
This leads to the local-mean BER for small l
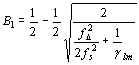 (13)
(13)
The effect of the ICI dominates over the AWGN for vehicle speeds
v > fs fc-1c Ö (2N0/PT Ts). (14)
Figure 2: Received power P0 (green), and the variances P1, P2, and P2 of the ICI (red) versus the normalized Doppler spread l for pT = 1.
 MATLAB | 
JavaScript |