Wireless Communication

Chapter: Wireless Propagation Channels
Section: Channel Models, Indoor Propagation

Estimating the RMS Delay Spread 

from the Frequency-Domain Level Crossing Rate

 Contributed by Klaus Witrisal  

The root-mean-square (RMS) delay spread is probably the most important single measure for the delay time extent of a multipath radio channel. Since the impulse response (IR) and the transfer function (TF) of a channel are related by the Fourier transform, it is intuitively understandable that the TF's magnitude shows more fades per bandwidth, the longer the IR.
 

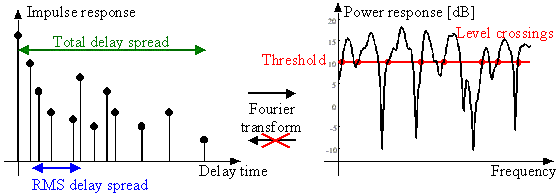
As shown by Witrisal et al. [2], [3], there exists a well-defined relationship between the so-called level crossing rate in the frequency-domain (LCRf) and the RMS delay spread (Trms), written as

    LCRf = Trms * f(K, r', u).    (1)

As seen from this equation, Trms and the LCRf are proportional, where the proportionality factor is a function of

For the LCRf at the RMS amplitude value of the channel transfer function, the factor f(K,r' = 1,u = 0) can be approximated by

 .

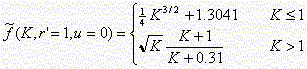Application to Channel Measurements

Equation (1) allows for the estimation of a complete set of wide-band channel parameters (average received power, Ricean K-factor, and RMS delay spread) from rather simple swept-frequency power measurements of the channel. (Note that the Fourier transform cannot be used to calculate an IR from a measured power response, due to the lack of phase information). The following measurement procedure is suggested: An observation bandwidth of 10/Trms (equivalent to the observation of approx. 20 level crossings) allows for estimating Trms at an accuracy in the order of 10 %. Higher bandwidths can enhance the accuracy. Alternatively, multiple measurements from within a small local area can be combined to increase the observation bandwidth without modifying the measurement equipment.

Other issues that should be considered when applying this method for channel investigations are:

 

 

next


Wireless Communication © Klaus Witrisal
Centre for Wireless Personal Communications (CEWPC)
TU-Delft, IRCTR
Mekelweg 4
NL-2628 CD Delft
The Netherlands

Phone: +31(0)15-27-87371
Fax: +31(0)15-27-84046
email: K.Witrisal@ITS.TUDelft.NL
 

References

  1. K. Witrisal, Y.-H. Kim, and R. Prasad, "RMS Delay Spread Estimation Technique Using Non-Coherent Channel Measurements," IEE Electronics Letters, vol. 34, no. 20, Oct. 1998, pp. 1918 – 1919
  2. K. Witrisal, Y.-H. Kim, and R. Prasad, "A New Method to Measure Parameters of Frequency-Selective Radio Channels Using Power Measurements," accepted for IEEE Transactions on Communications
  3. K. Witrisal, Y.-H. Kim, and R. Prasad, "Frequency-Domain Simulation and Analysis of the Frequency-Selective Ricean Fading Radio Channel," in Proc. PIMRC’98, Boston, Sept. 1998, pp. 1131 – 1135
  4. K. Witrisal, G. Landman, and A. Bohdanowicz, "Practical Application of a Novel Method for Estimating the RMS Delay Spread from Power Measurements," accepted for EPMCC 2001 (4th European Mobile Communications Conference), Vienna, Austria, Feb. 2001
  5. K. Witrisal, A. Bohdanowicz, "Influence of Noise on a Novel RMS Delay Spread Estimation Method ," in Proc. IEEE PIMRC'2000, London, Sept. 2000, pp. 560 – 566