| Wireless CommunicationChapter: Wireless Propagation Channels |
Contributed by Peter E. Leuthold and
Pascal Truffer
Several definitions exist for the scatter function of a multipath channel. Basically, these "parameters", "functions" and "profiles" describe the time and frequency dispersion of the channel. This contribution defines and discusses functions that defines delay spread and angle of arrival. For outdoor, vehicular channels, time dispersion is often a more useful parameter than angle of arrival, while for indoor systems with diversity, angle of arrival is more useful. Note however that if an antenna is in motion, there is a direct relation between angle of arrival and Doppler shift.
A description of the dispersive radio
channel can be based on the electric field delay-direction spread vector
defined
in [4]. The
vector 
denotes the MT antenna location, and 
and 
are the delay
and incidence direction variables, respectively, where is determined
by the azimuth 
and the coelevation 
in a spherical coordinate
system.
The vector can be
decomposed into a sum of M components each originating from a
hypothetical impinging wave:
The notation 
means that the number of active paths or
dominant waves varies with the location when the MT is moving along
the trajectory. Under far field conditions the vector has two components which correspond to
the vertical and horizontal polarization.
called
FDDSF. The CIR follows by
where 
is proportional to the field pattern of the MT antenna for
the considered polarization.
We now assume that over a sufficiently small area A the wave incidence constellation, i.e. the number of active paths, relative delay, angle of arrival and amplitude, remains approximately constant. Consequently, the spatial variations of the FDDSF mainly result from the changes of the phase of the wave components.
Within the area A the wave incidence constellation is characterized by the local power delay-direction profile (PDDP)
which may be presented in the SCRM as the product
In this equation, 
denotes the path loss for the distance
from the transmitter station to the area A and
is the local delay-direction scattering function
(DDScF) in A. Since the components in (1) are regarded as
independent we obtain with (4) the expression
that means each term is determined by the mean power 
, the mean
delay 
, the mean incidence direction 
and a
local scattering function which is considered to
be identical for all components. Obviously, the variables M,
, , and are random variables.
Table 2: Description of the primary random variables M, , (delay
spread 
)
Their specification is given in
Table 2 [2] with the
exception of which will be discussed later on.
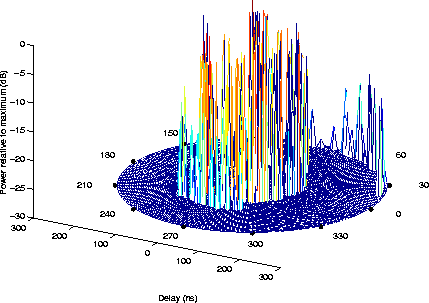
Figure: Local PDDP generated with the SRCM
Figure 1 presents a realization of the local
PDDP obtained with the SRCM. In this case as well as for the next
Figures 2 to 6 the
following parameters have been chosen: carrier frequency 5.2 GHz, MT
velocity 1 m/s, delay spread 
. Such a
situation is typical for a small room environment.
Taking the expectation of the local DDScF over a class C of environments, i.e. a large room, yields the global DDScF
In accordance with the assumptions in Table 2 this function takes the form
where the global delay scattering function 
(DScF) follows integrating 
with respect to
. It is reasonable to choose the global DScF as an
exponentially decaying function
that means the scattered power decreases with increasing delay. With
regard to the channel simulation the global DDScF according
to (7) and (8) can be considered as a target function which represents the
expectation of Gaussian processes with the standard deviation
and
, respectively.
Figure 2 shows the successive approximation of the global DScF by the average of local DScFs.
