

|
Wireless CommunicationChapter: Analog and Digital
Transmission
|
In MC-CDMA, after recovery of the subcarriers, the signals at the output of the FFT have to be 'unspread', by applying the inverse code matrix. However some weighing is needed to optimize performance and to mitigate the effects of the channel. At this point we restrict ourselves to the class of (linear) receivers which make decisions based on linear combinations of all subcarrier signals, as e.g. in Figure 3. We explicitly introduce the FFT, the inverse code matrix C-1 and a generic weigh matrix W. This allows us to address a simple implementation for the receiver, where the weighing reduces to a simplified adaptive diagonal matrix, while the FFT and C-1 are nonadaptive, and can be implemented efficiently using standard butterfly topologies.
Two policies for the setting of the weigh matrix W with elements wn,m are intuitively appealing and have been proposed e.g. in [12].
A joint optimization can be derived from the following MMSE model [21]. It reduces the joint effects of noise, MUI and ICI. The Minimum Mean-Square Error Estimate of the user data is equal to the conditional expectation EB|Y. We can rewrite this as
EB|Y = EC-1A|Y = C-1EA|Y (15)
Here the expectation E is over all instances of the modulation, but keeping the channel fixed. It shows that without loss of performance one can estimate the modulation of each subcarrier as A, and then perform an inverse of the code matrix, using B = C-1A for the user data. Let A be a linear combination of Y, namely A = WY. The optimum choice of matrix W follows from the orthogonality principle that the estimation error is uncorrelated with the received data, viz., E(A - A)YH = 0N with 0N an all-zero matrix of size N by N. Thus we arrive at W = E[AYH] RYY-1, for the optimum estimation matrix. Here Y = HA + N, where channel matrix H has the components Hnm = b nm. In such case,
E(AYH) = E(A(HA)H) + E(ANH) = EAAHHH = C EBBHCHHH = HH. (16)
Also, RYY, the covariance matrix of Y, becomes
RYY = EYYH = H E(AAH) HH + ENNH = HHH + N0 TsIN (17)
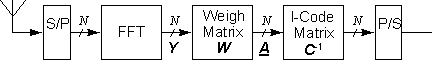
Figure: Linear receiver architecture for MC-CDMA
Inversion is needed to find the MMSE of the signal in the presence of noise, MUI and ICI. For simplicity, we initially review the special case of a channel without Doppler spread, thus with H = Ts diag(b 0,0, ... b N-1, N-1), as it was proposed in [21]. Then E(AYH) reduces to
E[AYH] = diag(b 0,0*Ts, b 1,1* Ts, .., b N-1,N-1*Ts) (18)
and
RYY = diag(b 0,0b 0,0* Ts2 + N0Ts , b 1,1b 1,1*Ts2 +
N0Ts, .., b N-1,N-1b N-1,N-1*Ts2 + N0Ts). (19)
We observe that W reduces to a diagonal matrix with elements [21]
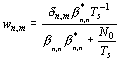 (20)
(20)
That is, each subcarrier is weighed by a factor which only depends on the signal strength in that subcarrier and the noise, we interpret this as an automatic gain control and a phase corrector. The effect of adaptive (non-ideal) tracking of subcarrier amplitudes in channels that are sufficiently slowly fading to avoid excessive Doppler was addressed in [22].
In the more general case of time-varying channels with ICI implementation of this MMSE solution is quite involved because W does not reduce to a diagonal matrix. This implies that the optimum filter requires a (channel-adaptive) matrix inversion. Techniques have been studied to (blindly) estimate channel parameters in real-time, e.g. [23, 24]. Mostly, such studies assume a limited number of (dominant) propagation paths (small Iw), so in this respect these differ from our Rayleigh model. In practice, it may not always be feasible or economic to estimate all b m,n accurately, invert the covariance matrix in real-time, while adapting fast enough for the time-variations of the channel.
We propose a receiver that estimates only b n,n, but no off-diagonal terms b m,n with m ¹ n. We take the weight settings of W to be as in (20), except that the noise N0/Ts is replaced by the joint contribution from noise and ICI. In the next section we calculate the BER. In the appendix, we study the statistical behavior of b n,n and wn,n for Rayleigh channels with Doppler, in particular Mij defined as Mij = Ech |b n,n|i |wn,n|j. In contrast to most previous expressions in this section, the expectation is taken over all channels, and denoted as Ech. We exploit that |b n,n| is Rayleigh with mean square value P0. See: MATLAB Code