

|
Wireless CommunicationChapter: Analog and Digital
Transmission
|
This section addresses the local-mean BER B1. For MC-CDMA (but not for OFDM), the BER B0 for one specific user signal converges to the local-mean BER if the number of subcarriers is sufficiently large and the transmit bandwidth largely exceeds the coherence bandwidth. In section 6, simulations are used to verify the accuracy this approximation and to investigate the behaviour for systems with fewer subcarriers. The decision variable for user bit 0, after combining all subcarrier signals consists of
![]() (21)
(21)
where x0 is the wanted signal, xMUI is the multi-user interference (due to imperfect restoration of the subcarrier amplitudes), xICI is the intercarrier interference (due to crosstalk b m,n between an and ym), and xnoise is the noise.
(22)
(23)
The variance of x0 vanishes for large N, i.e., the system sees a non-fading channel.
(24)
(25)
(26)
(27)
(28)
Thus,
(29)
- The ICI contribution stems from crosstalk between subcarriers. Signal components which are present in an = S k ck[n]bk are spilled into ym = yn+D , with strength b n+D ,n. In the receiver, these are weighted by wn+D ,n+D and unspread by c0[n+D ].
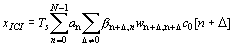
(30)
Inserting an = S k ck[n]bk and interchanging the sequence of the summings
(31)
Thus,
(32)
The square of the triple sum simplifies because of Ebk bj*= d kj and Ech b i,j b k,l = d ijd kl and similar properties. We take, for reasons soon to be discussed,
E[c0[n] ck[n - m]]2 = N-2. So,
(33)
Thus
s ICI2 = S D ¹ 0pD M02 Ts2. (34)
Here the question arises whether a system designer can chose the spreading matrix C such that the ICI is mitigated. This poses requirements on the cross-correlation S c0[n]ck[n-m]. It is the time-frequency dual of the well known problem of finding good codes for asynchronous DS-CDMA with good cross and autocorrelation properties to combat delay spread. Walsh-Hadamard codes have no particular properties to achieve good autocorrelation properties, and their auto-correlation behaviour can be approximated by the behavior of randomly chosen codes. Here the situation here more involved, because each term c0[n]ck[n-m] is multiplied by b m,n and wn,n, which are complex valued with random arguments. Thus, even if the code had good auto-correlation properties, these erode the corresponding attenuation of ICI.
s noise2 = N M02 N0Ts. (35)
Since we consider ensembles of many different channels, xMUI,
xICI and xnoise are zero-mean complex Gaussian.
So, the local-mean BER becomes![]() , with
, with
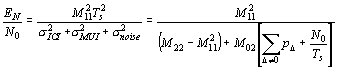 (36)
(36)
We introduce the figure of merit z , and rewrite (36) as EN/N0 = z P0 Ts/N0. Thus z is a system parameter, which gives the improvement of MC-CDMA in a Rayleigh fading channel, over narrowband transmission in a non-fading channel. For very poor local-mean signal to noise ratios (large P0 Ts/N0), the noise largely dominates over the MUI, and the MC-CDMA MMSE receiver acts mainly as a maximum ratio combiner Since wn,n @ b n,n/ N0,
M11 ® E b n,n2/N0 = P0 / N0
M02 ® E b n,n2/N02 = P0 / N02
M22 ® E b n,n4/N02 = 2P02 / N02
and z tends to unity (0 dB).