Wireless Communication Chapter: Analog and Digital Transmission Section: Multi-Carrier Modulation, OFDM, Effect of Doppler

Discrete-Frequency Channel Model for OFDM

This page develops a model for a channel representation starting from the classic multipath description, using a collection of I_w reflected waves. Each wave has its particular Doppler frequency offset w _i, path delay T_i and amplitude D_i. The frequency offset lies within the Doppler spread -2p f_D < w _i < 2p f_D , with f_D = v_s f_c/c. Here v_s is the velocity of the mobile antenna, c is the speed of light and the carrier frequency is w _c = 2p f_c. More precisely, the Doppler shift of the i-th wave is w _i = (2p v_s/c) f_c cos(q _i) with q _i the angle of arrival. Let f_s denote the spacing between the adjacent subcarriers and w _s = 2p f_s. The received signal equals

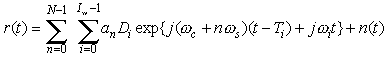
here n(t) is additive white Gaussian noise. We will denote the vector of modulation symbols as A = [a₀, a₁, ...a_N-1]^T. The transmit energy per subcarrier is E_N = E |a_n|². Not all reflected waves are individually ‘resolvable’, that is, a receiver sampling in a time-window of finite duration will only see the collective effect of multiple reflected waves within a certain time-frequency window.

The narrowband mobile channel model can be compacted into a complex received amplitude that is time varying. We rewrite the received signal as

where the time-varying channel amplitude V_n(t) at the n-th subcarrier is

A Tayler expansion is V_n(t) = v_n⁽⁰⁾ (t₀)+ v_n⁽¹⁾ (t₀) (t - t₀) + v_n⁽²⁾ (t₀) (t -t₀)² / 2 + .. .

See an animation of a Rayleigh fading complex amplitude. Have the amplitude plotted for you live on screen, and imagine what values the derivatives take on.

Here v_n^(q) (t₀) denotes the q-th derivative of the amplitude with respect to time, at instant t = t₀. If the Doppler spread is much smaller than the frequency resolution of the FFT grid, we may restrict our analysis to zero and first order effects. In a Rayleigh channel, v_n^(q) is zero-mean complex Gaussian for any n and q. To characterize the channel, we are interested in the covariance of variables v_n^(p) and v_m^(q), viz., Ev_n^(p)v_m*^(q), where * denotes the complex conjugate. In [20], we have derived this for an exponential delay spread and a uniform angle of arrival. The covariance becomes, for p + q even, (3)

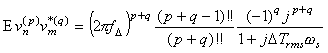
and Ev_n^(p)v_m*^(q) = 0 for p + q is odd.

Discrete-Frequency Link Model

In OFDM, a frame of N symbols is detected by taking N samples and performing an FFT. In other words, detection of the signal at subcarrier m occurs by correlation with a complex sinusoid having the frequency of the m-th subcarrier, viz., exp{-jw _ct-j(m-D _f)w _st } during the symbol duration NT. Here D_f is the frequency offset normalized to the subcarrier spacing w _s. In the sampling process, the receiver makes a timing error _t, where D _t is the time offset normalized to a sample interval T = (N f_s)- ¹. That is, it samples at t = D_t, D_t + T, D_t + 2T, ... . We assume that cyclic prefixes avoid any interframe interference. We use Y as the vector of length N to denote the output of the FFT in the receiver. The m-th output of the FFT is found as

Here, m = 0, 1, ..., N - 1 and Y = [y₀ , y₁, ... , y_N-1]^T. We observe that w _sT = 2p/N. We introduce the OFDM system parameter x_D^(q), defined as

to describe the signal transfer over the q-th derivative of the amplitude at subcarier n to the (n+D )-th receive subcarrier. This allows us to rewrite y_m as follows:

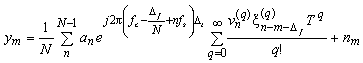
In particular, we will consider the first two terms of the expansion, and we denote c_D = x_D⁽⁰⁾ and z_D = x_D⁽¹⁾. So,

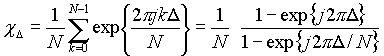
For integer D , cD reduces to d_D , which is just a confirmation that subcarriers (with a nonfading amplitude) are orthogonal. Note further that

for integer and non-zero D , we see that

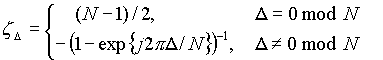
Roughly speaking z_D / z₀ » (jp D )^-1, with D = 1, 2, 3, ...., so the ICI reduces slowly with increasing subcarrier separation. Relatively many subcarriers make a significant contribution to the ICI. We define vector V = [v₀, v₁, .., v_N-1] for the subcarrier amplitudes and V’ = [v₀⁽¹⁾, v₁⁽¹⁾, .., v_N-1⁽¹⁾]^T for the derivatives.

For an ideally synchronizing receiver, i.e., with D_t = 0 and D_f = 0,, the received signal Y can compactly be written in Discrete Frequency domain as,

with DIAG(X) the diagonal matrix composed of the elements of vector X, and

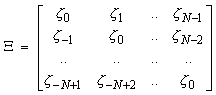
Not all terms in X address ICI: In the expression, the diagonal terms z₀ carry signal components from the n subcarrier to the n-th subcarrier, so in fact the receiver sees a signal amplitude of (c₀ v_n + ^z₀ T v_n⁽¹⁾)a_n. To address this in the following calculations we define X^* = X - z₀ I_N. The wanted signal component in a conventional receiver equals V+z₀ V’T, which in practice closely approximates V, except in deep fades.

Figure 1 depicts the channel and receiver in the discrete frequency domain. Thus, the FFT is not drawn explicitly. In a conventional system, W represents the equalizer, or automatic gain control per subcarrier, to compensate for fading on the subcarriers.

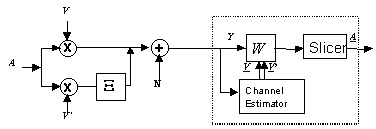
Figure 1: Discrete-Frequency representation for the Doppler multipath channel and a (feedforward) OFDM receiver

Next: how to build a receiver based on this principle?

Wireless Communication © Jean-Paul M.G. Linnartz, 2001.

The key ideas of this page have been published first in: J.P.M.G. Linnartz and A. Gorokhov, "New Equalization approach for OFDM over dispersive and rapidly time varying channel", PIMRC 2000, London.