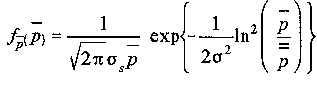Shadowing

Experiments reported by Egli in 1957 showed that, for paths longer than a few hundred meters, the received (local-mean) power fluctuates with a 'log-normal' distribution about the area-mean power. This means that the local-mean power expressed in logarithmic values, such as dB or neper, has a normal (i.e., Gaussian) distribution. The probability density function (pdf) of the local-mean power is thus of the form

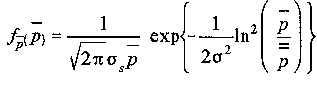
where sigma is the logarithmic standard deviation of the shadowing, expressed in natural units. The standard deviation expressed in dB is found as 4.34 times the sigma in natural units.

Depth of Shadowing

For average terrain, Egli reported a logarithmic standard deviation of about 8.3 dB and 12 dB for VHF and UHF frequencies, respectively. Such large fluctuations are caused not only by local shadow attenuation by obstacles in the vicinity of the antenna, but also by large-scale effects leading to a coarse estimate of the area-mean power.

This log-normal fluctuation was called 'large-area shadowing' by Marsan, Hess and Gilbert; over semi-circular routes in Chicago, with fixed distance to the base station, it was found to range from 6.5 dB to 10.5 dB, with a median of 9.3 dB. Large-area shadowing thus reflects shadow fluctuations if the vehicle moves over many kilometres.

In contrast to this, in most papers on mobile propagation, only 'small-area shadowing' is considered: log-normal fluctuations of the local-mean power over a distance of tens or hundreds of metres are measured. Marsan et al. reported a median of 3.7 dB for small area shadowing. Preller and Koch measured local-mean powers at 10 m intervals and studied shadowing over 500 m intervals. The maximum standard deviation experienced was about 7 dB, but 50% of all experiments showed shadowing of less than 4 dB.

Implications for Cell Planning

If one extends the distinction between large-area and small-area shadowing, the definition of shadowing covers any statistical fluctuation of the received local-mean power about a certain area-mean power, with the latter determined by (predictable) large-scale mechanisms. Multipath propagation is separated from shadow fluctuations by considering the local-mean powers. That is, the standard deviation of the shadowing will depend on the geographical resolution of the estimate of the area-mean power. A propagation model which ignores specific terrain data produces about 12 dB of shadowing. On the other hand, prediction methods using topographical data bases with unlimited resolution can, at least in theory, achieve a standard deviation of 0 dB. Thus, the standard deviation is a measure of the impreciseness of the terrain description. If, for generic system studies, the (large-scale) path loss is taken of simple form depending only on distance but not on details of the path profile, the standard deviation will necessarily be large. On the other hand, for the planning of a practical network in a certain (known) environment, the accuracy of the large-scale propagation model may be refined. This may allow a spectrally more efficient planning if the cellular layout is optimised for the propagation environment.

Exercise

The area-mean power corresponds to the logarithmic average of the received local mean power. Show that the linear average and higher-order moments of the local-mean power are of the form

E[power^n] = (area-mean power)^n exp(n^2 sigma^2/2)

The linear average is thus not identical to the area-mean power, except in the limiting case of sigma = 0.

With shadowing, the interference power accumulates more rapidly than proportionally with the number of signals. The accumulation of multiple signals with shadowing is a relevant issue in the planning of cellular networks.